Spin Inversion : deterministic & chaotic superposition
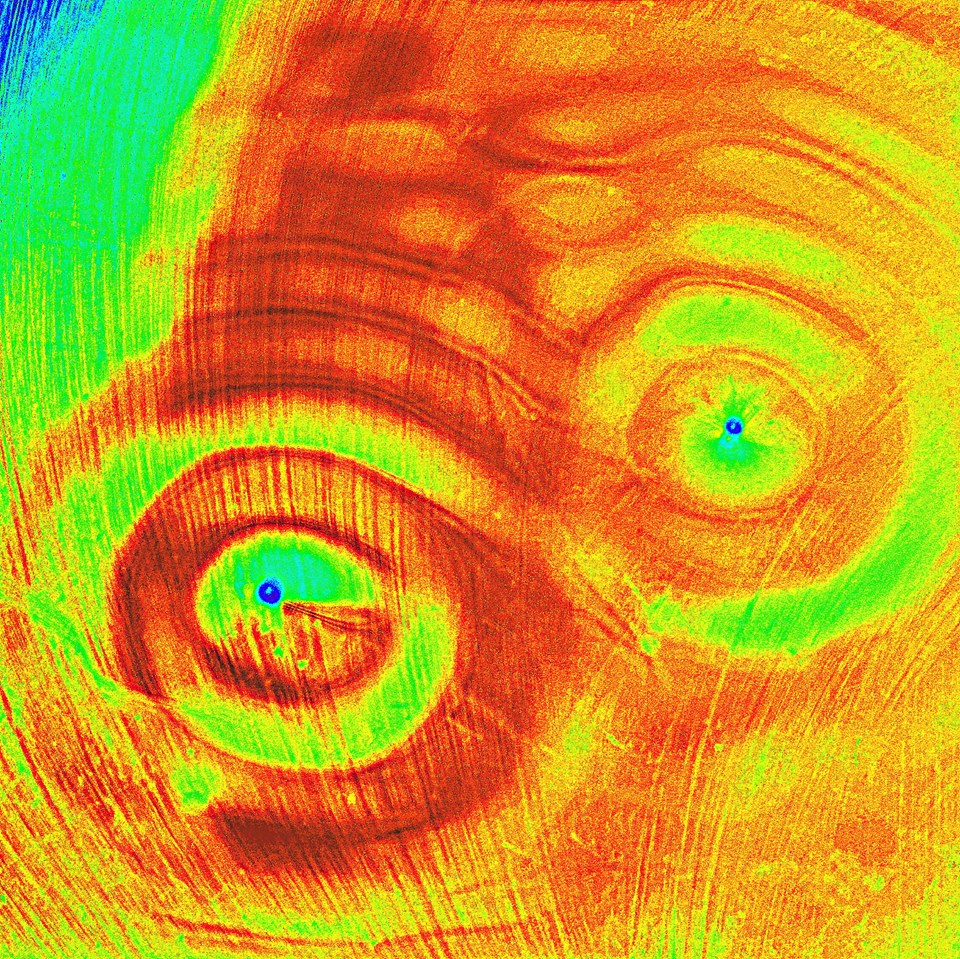
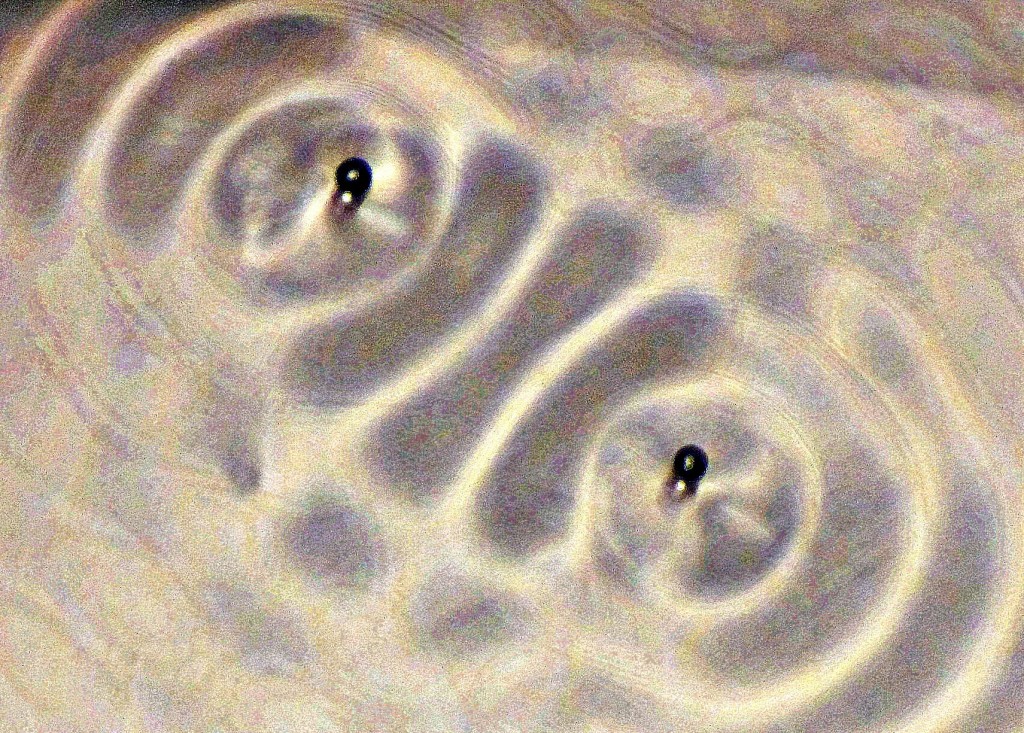
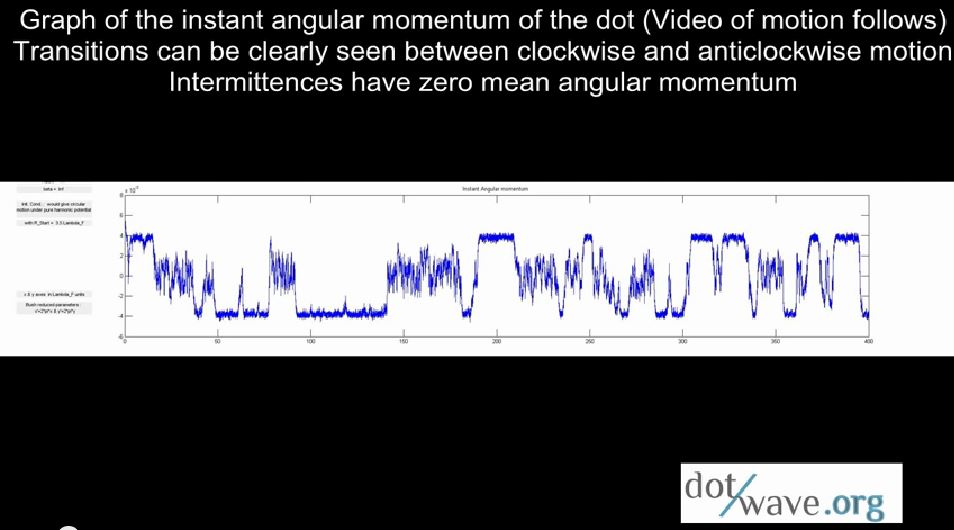
On this purely deterministic superfluid simulation of a dotwave in a harmonic potential ( dot attached to a spring, no viscous dissipation, D=0), the dot has successive clockwise and anti-clockwise circle-like motions, separated by intermittences with null mean angular momentum
A Hydrodynamic Pilot Wave Model : RIO 2014
Analysis of currrent state of the art modelling
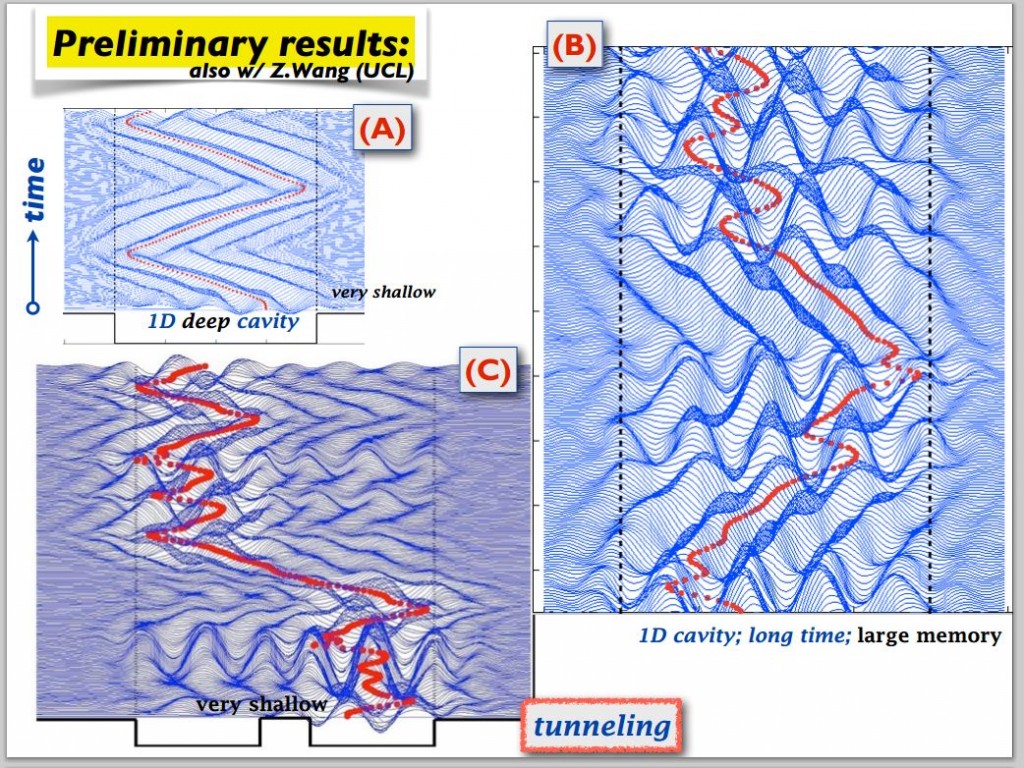
Reflexions in a 1D Cavity
Computer simulations
(proceedings of RIO 2014 Â workshop)
http://www.personal.psu.edu/alm24/IMPA/talks/IMPANachbin.pdf
Simons Foundation talks about the walker research
An interesting (almost) state of the art review with historical perspectives and some  (negative) nobel prizes insights.
http://www.simonsfoundation.org/quanta/20140624-fluid-tests-hint-at-concrete-quantum-reality/
Numerical simulation : how it is done
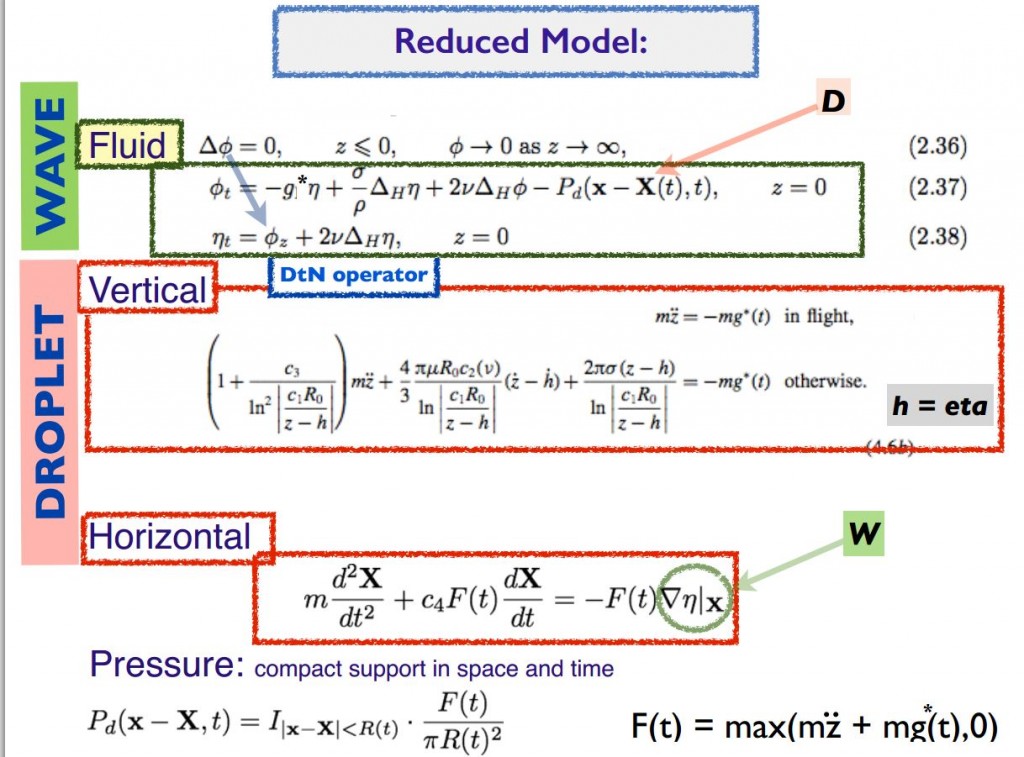
In this PDF, you will find the equation of motion used in the numerical simulation, based on the work of BUSH et al. from the MIT team.
DotWaveSimulation
Surfer DotWave attached to a spring moving with no viscosity
Surfer attached to a spring moving with no viscosity
Integration of motion equation is done continuously via matlab DELAY DIFERENTIAL EQUATION (ddesd) solver
Hence, the dot “reads” continuously the value of the field
In the mean time, the dot “writes” to the field evry T_F (that is a “bounce”) : at each bounce, a local wave field represented by a Bessel JO function is created, which is then slowly damped (That is the memory Me parameter)
Interferences between the waves created by the last previous 300 bounces (THAT IS THE CUTOFF parameter) are computed at each integration step to obtain the shape of the wave and the motion of the dot.
Superposition, Decoherence, Schrodinger’s Cat and other magical lies my professors told you.
There is a good reason we are all fascinated with the walkers experiment. For any student of Quantum Mechanics (QM), the interpretation of the QM formalism is at first a puzzling proposal. There is a large suspension of disbelief that needs to take place. Simply put it is ‘counter intuitive’ and most people “shut up and calculate” essentially bowing to the myth that “QM is just very weird”.
How can things be in ‘several states’ at the same time. QM matter must be of a different, slightly magical, nature. It is perhaps best exemplified by paradox of the Schrodinger cat that is both dead and alive, supposedly at the same.
In this post we will apply the formalism of walkers, an emergent model of QM dynamics that comes about from the association of a particle and a wave and show how it sheds a new light on the fundamental interpretation of QM and show that in this interpretation, the cat is simply always dead.
We will also use this formalism to shed light on the typically QM notion of coherence and decoherence.
Particle in a box – DotWave Self-Interference tracking and statistics
Wave particle in a 1-D box, tracking and statistics
particle-Wave in a ring : a Dotwave Collisionner
Could such a setup be used to create a microfluidic “in-a-droplet” chemical reactor mixer ?
The Feynman Lectures on Physics : Quantum behavior
Where it all started …
Controlled double-slit electron diffraction : reproduction of the famous Feynman 1965 thought experiment.
Bach, R., Pope, D., Liou, S. H., & Batelaan, H. (2013). Controlled double-slit electron diffraction. New Journal of Physics, 15(3), 033018.
http://iopscience.iop.org/1367-2630/15/3/033018/pdf/1367-2630_15_3_033018.pdf
And some movies of the interference pattern build-up :
http://iopscience.iop.org/1367-2630/15/3/033018/media
The famous Feynman thought experiment reproduced ! ((cf. Feynman Lectures on Physics, vol III, ïŹgures 1â3,))
Confinement of electrons to quantum corrals on a metal surface
Crommie, M. F., Lutz, C. P., & Eigler, D. M. (1993). Confinement of electrons to quantum corrals on a metal surface. Science, 262(5131), 218-220.
http://users.phys.psu.edu/~rick/MATH/LECTURES/LECT13/PDF/eigler_circular_corral.pdf
Classical analog of quantum eigenstate – Orbits and trajectory level
On this video, you’ll see :
– How 2 dotwaves can synchronize on 2 orbits
– How a dotwave can change his orbit (with a little help from the experimentator)
Video shot with a 30 Hz camera, at a forcing frequency of 60 Hz, hence not much stroboscopic flickering
The bath is excited just at the Faraday llevel, or slighly upper.
Dotwave in a box : emergence of normal mode
On this video, the walking droplet is confined in a small cavity (Approx. 6 to 8 times the faraday wavelength)
We observe the emergence of several normal modes of vibration of a walking droplet in a circular corral.
At first, the movement seems “random”, then, the whole wave-particle system synchronizes, and starts turning alltogether.
Differrent modes are possible, with different radius for the droplet trajectory : on this video we see a mode with the droplet on a large radius trajectory, and also a mode where the droplet is on a short radius trajectory
Its seems that thoses radius coincide with with the knots ofs thefaraday standing waves of the cavity, hence we have a quantization of the radius of the different trajectories.
How it is done : DIY Cymatronics
A Transparent plate is mounted  (via magnets) to three loud peakers serial-connected to an amplifier delivering a sinus signal.
Silicon oil ( with viscosuity 20 Cst) Â is put on the transparent plate.
A Â point source light is collimated, goes through the oil
A mirror placed below redirects the light beam to tha camera.
NB : it is not easy to set up this light system : the light source muste precisely tuned at the focal point of the lens.
Vibration modes of a walking droplet trapped in a small circular box
When a walking droplet is trapped in a small box, the waves that it has generated extends to the whole frame.
Thus those waves  can resonate  and form normal modes of vibration inside the cavity.
The droplet is then forced to move according to this normal wave field
2 walking droplets getting attracted
When  two walking droplets start turning around each other, the distance between them is n times the  wavelength (with n an integer) plus a constant.
Atomic view looks like walking droplets ?
Bouncing and walking droplet
Image from D. Terwagne, see : http://walkingdroplet.com/the-role-of-deformations-in-the-bouncing-droplet-dynamics/
Frame of IBM latest atomic movie