Goal of the experiment :
A walking droplet is placed in a square box, at the onset of Faraday thresold.
The trajectory of the droplet is mapped.
In the long time limit, does a self-interference pattern appear ? what’s its shape ? How does it relate to the square cavity surface wave eigen-modes ?
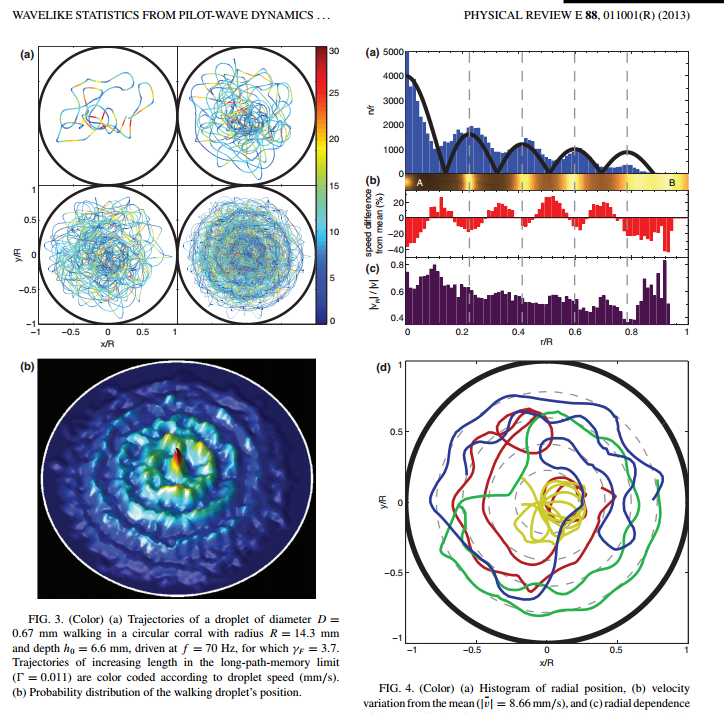
cf. experiment by Bush et al. : in a circular corral
http://dotwave.org/wavelike-statistics-from-pilot-wave-dynamics-in-a-circular-corral/
In short, we try to reproduce the experiment of Bush et al, but in a square box.
First result :
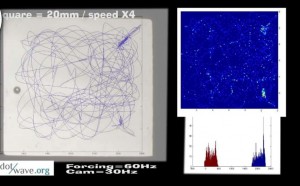
A walking droplet in a square cavity shows random motion, but with time, its trajectory is building a statistic reminiscent of the resonant mode of the cavity.
This can be seen by the naked eye in this movie excerpt :
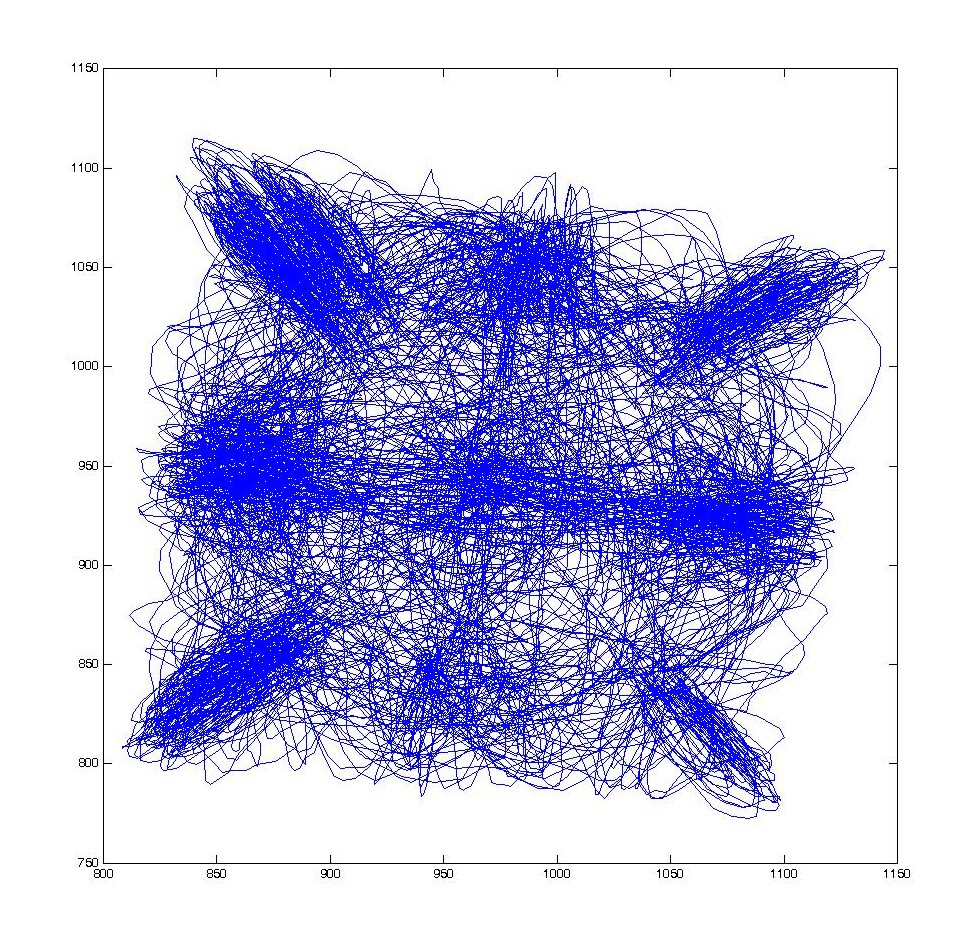
This is then confirmed with optical tracking measurment of the trajectory :
Trajectory of the walking droplet
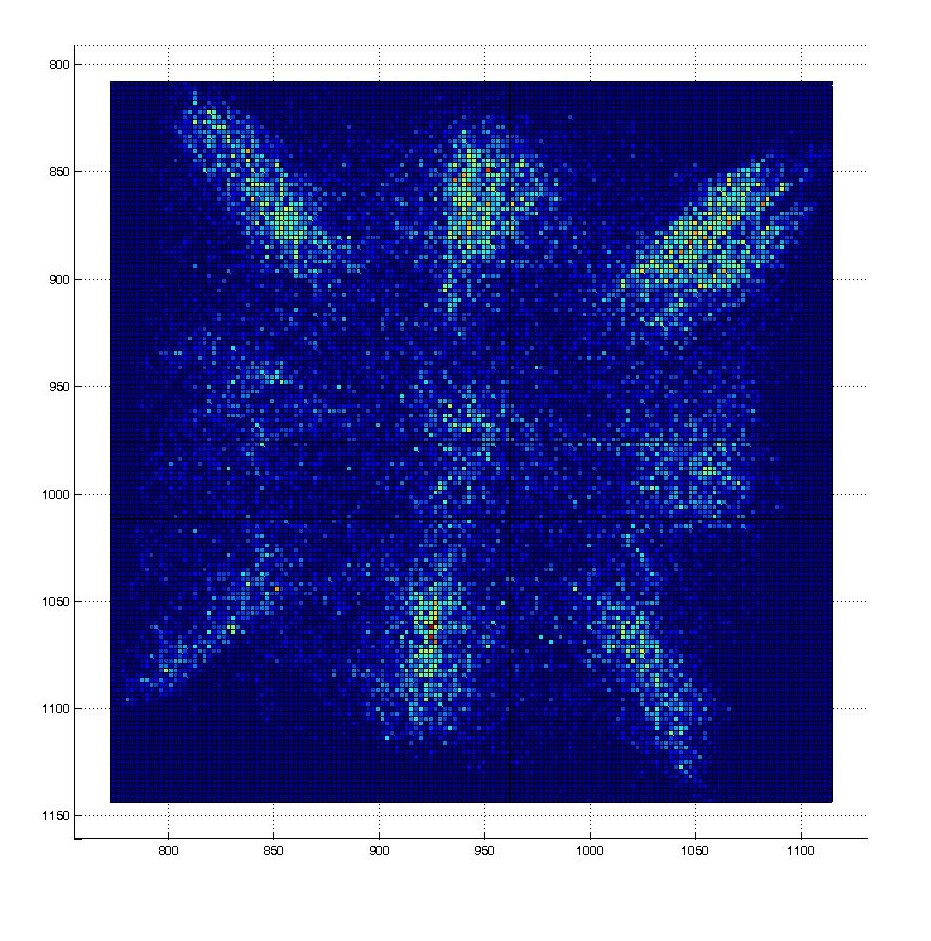
The position distribution (~probability density) is then computed :
Probabilty density
PDF Version of this résumé :
Emergent quantization of trajectories in a square box
what if we assume we have
something like this instead of the oil?
All this experiement is about is … analogy 🙂
well, according to the method, now it’s time for guessing some hypotesis/axioms, on which to build a model to try explain/motivate the analogy
let alone analogies should also bring more…
in switching from one context to the other, some behaviours are replicated/preserved: there should be a semantical simmetry and a semantical invariant, IMHO
are you happy with just having a set of analogies to show up?
I wouldn’t…
best wishes
corrado
Well, smarter people out there are trying to buid up theories on top of this experiment. I am just a sunday hoobyist …
me too!
but I also like playing with axioms and physics theories, especially from a semantical/epistemological perspective…
thx for your replies
From an epistemological point of you, the whole “walking droplet adventure” is worth studying : This object was unknown until 2005. So you, as a human, are able to read all bibiography about the subject, and contemplate how knowledge is being built, using the scientific method.
That contemplation in itself is quite fullfilling for the science lover 🙂
yep but…
Tristo è
quel discepolo
che non
avanza il
suo maestro
(Leonardo Da Vinci)
don’t be sad!
Mama mia 🙂 (It took me one week to understand your italian citation (and I am half italian !))
To me this is the answer.
GR has enough interesting behaviour to create physics.
Can a sub-quantum medium be provided by General Relativity?
http://iopscience.iop.org/article/10.1088/1742-6596/701/1/012023
–Tom
Thnakk you your website gravityphysics.com is quite interesting as well as your paper 🙂
Have you ever attended EmQm conferences in Vienna ?
Thanks. I attended EmQM 2015 last year. I had a poster there. http://iopscience.iop.org/article/10.1088/1742-6596/701/1/012023
–Tom