Perrard, S., Labousse, M., Fort, E., & Couder, Y. (2014). Chaos driven by interfering memory. Physical review letters, 113(10), 104101.
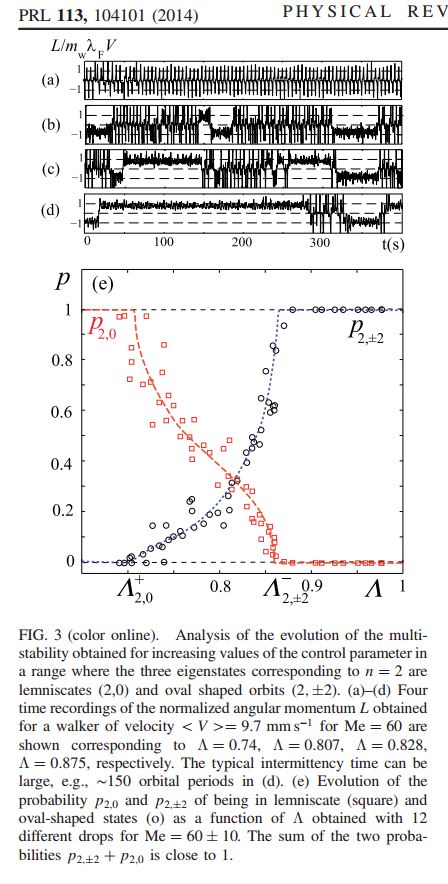
The transmission of information can couple two entities of very different nature, one of them serving as a memory for the other. Here we study the situation in which information is stored in a wave field and serves as a memory that pilots the dynamics of a particle. Such a system can be implemented by a bouncing drop generating surface waves sustained by a parametric forcing. The motion of the resulting “walker” when confined in a harmonic potential well is generally disordered. Here we show that these trajectories correspond to chaotic regimes characterized by intermittent transitions between a discrete set of states. At any given time, the system is in one of these states characterized by a double quantization of size and angular momentum. A low dimensional intermittency determines their respective probabilities. They thus form an eigenstate basis of decomposition for what would be observed as a superposition of states if all measurements were intrusive
https://hal.archives-ouvertes.fr/hal-01061415/document