Statistical projection effects in a hydrodynamic pilot-wave system
ABSTRACT :
“Millimetric liquid droplets can walk across the surface of a vibrating fluid bath, self-propelled through a resonant interaction with their own guiding or ‘pilot’ wave fields. These walking droplets, or ‘walkers’, exhibit several features previously thought to be peculiar to the microscopic, quantum realm. In particular, walkers confined to circular corrals manifest a wave-like statistical behaviour reminiscent of that of electrons in quantum corrals. Here we demonstrate that localized topological inhomogeneities in an elliptical corral may lead to resonant projection effects in the walker’s statistics similar to those reported in quantum corrals. Specifically, we show that a submerged circular well may drive the walker to excite specific eigenmodes in the bath that result in drastic changes in the particle’s statistical behaviour. The well tends to attract the walker, leading to a local peak in the walker’s position histogram. By placing the well at one of the foci, a mode with maxima near the foci is preferentially excited, leading to a projection effect in the walker’s position histogram towards the empty focus, an effect strongly reminiscent of the quantum mirage. Finally, we demonstrate that the mean pilot-wave field has the same form as the histogram describing the walker’s statistics.”
Sáenz, P. J., Cristea-Platon, T., & Bush, J. W. (2018). Statistical projection effects in a hydrodynamic pilot-wave system. Nature Physics, 14(3), 315.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2017/12/Saenz-NatPhys-2017-.pdf
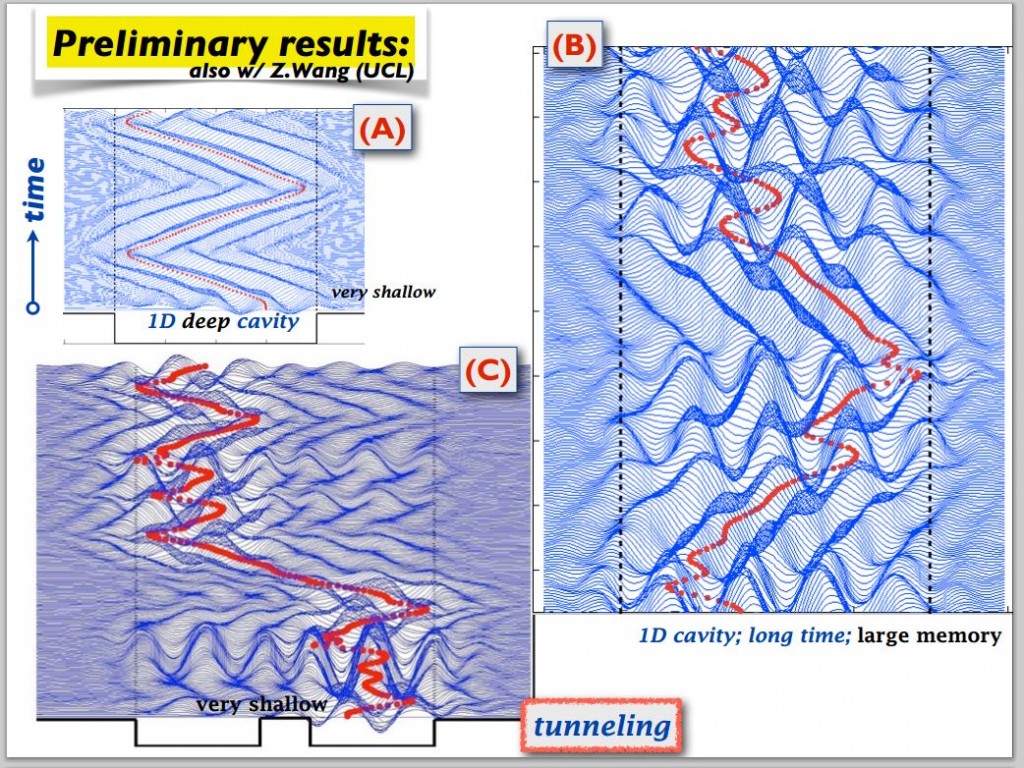
Tunneling with a hydrodynamic pilot-wave model
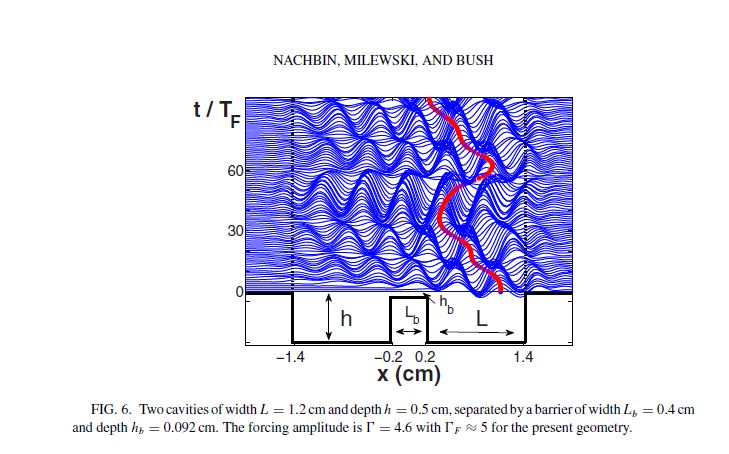
ABSTRACT : “Eddi et al. [Phys. Rev Lett. 102, 240401 (2009)] presented experimental results demonstrating the unpredictable tunneling of a classical wave-particle association as may arise when a droplet walking across the surface of a vibrating fluid bath approaches a submerged barrier.We here present a theoreticalmodel that captures the influence of bottom topography on this wave-particle association and so enables us to investigate its interaction 2 with barriers. The coupledwave-droplet dynamics results in unpredictable tunneling events.
As reported in the experiments by Eddi et al. and as is the case in quantum tunneling [Gamow, Nature (London) 122, 805 (1928)], the predicted tunneling probability decreases exponentially with increasing barrier width. In the parameter regimes examined, tunnelingbetween two cavities suggests an underlying stationary ergodic process for the droplet’s position.”
Nachbin, A., Milewski, P. A., & Bush, J. W. (2017). Tunneling with a hydrodynamic pilot-wave model. Physical Review Fluids, 2(3), 034801
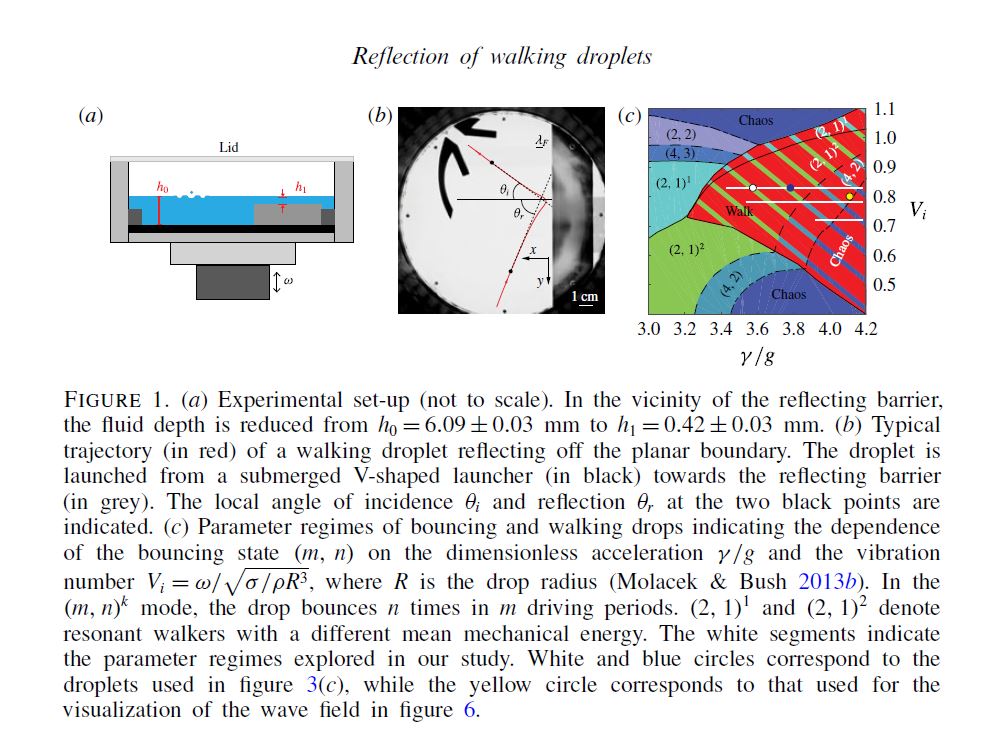
Non-specular reflection of walking droplets
Abstract : Since their discovery by Yves Couder and Emmanuel Fort, droplets walking on a vibrating liquid bath have attracted considerable attention because they unexpectedly exhibit certain features reminiscent of quantum particles. While the behaviour of walking droplets in unbounded geometries has to a large extent been rationalized theoretically, no such rationale exists for their behaviour in the presence of boundaries, as arises in a number of key quantum analogue systems. We here present the results of a combined experimental and theoretical study of the interaction of walking droplets with a submerged planar barrier. Droplets exhibit non-specular reflection, with a small range of reflection angles that is only weakly dependent on the system parameters, including the angle of incidence. The observed behaviour is captured by simulations based on a theoretical model that treats the boundaries as regions of reduced wave speed, and rationalized in terms of momentum considerations.
Pucci, G., Sáenz, P. J., Faria, L. M., & Bush, J. W. (2016). Non-specular reflection of walking droplets. J Fluid Mech, 804, R3.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2016/09/Pucci-JFM-2016.pdf
Onset of chaos in orbital pilot-wave dynamics
Abstract : We examine the orbital dynamics of droplets self-propelling along the surface of a vibrating bath. Circular orbital motion may arise when the walking droplet is subjected to one of three external force fields, the Coriolis force, a simple harmonic force, and a Coulomb force. Particular attention is given to a theoretical characterization of the onset of chaos that accompanies the destabilization of such circular orbits.
Tambasco, L., Harris, D., Oza, A., Rosales, R., & Bush, J. (2015, November). Onset of chaos in orbital pilot-wave dynamics. In APS Meeting Abstracts.
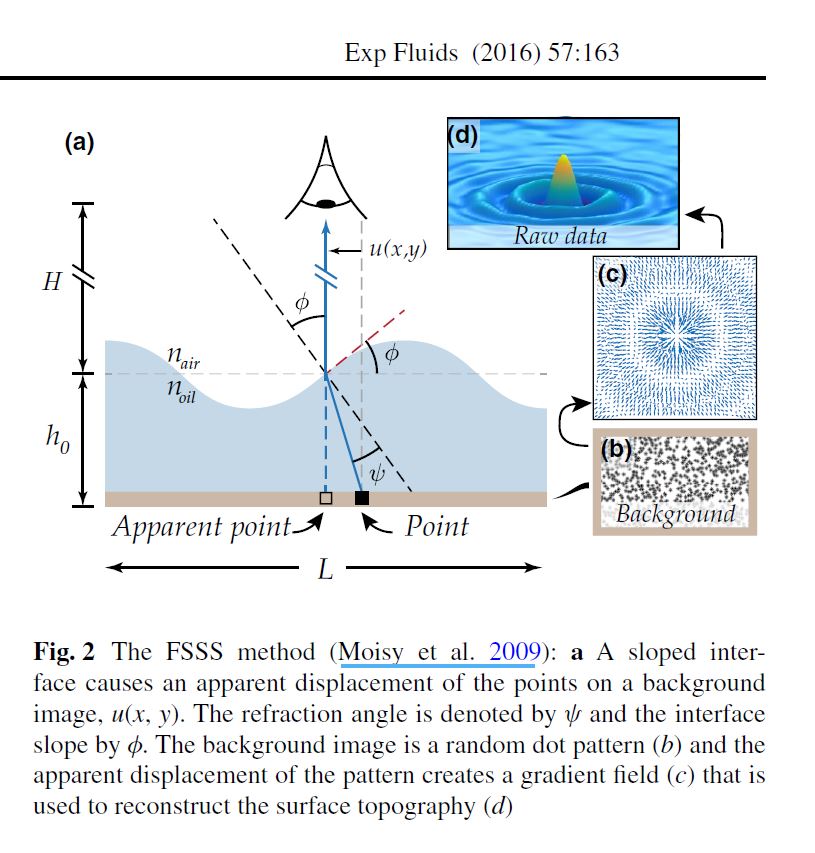
Surface topography measurements of the bouncing droplet experiment
A technical entry by the american team reproducing the synthetic Schlieren free surface measurment already implemented successfully by the Paris Team.
Damiano, A. P., Brun, P. T., Harris, D. M., Galeano-Rios, C. A., & Bush, J. W. (2016). Surface topography measurements of the bouncing droplet experiment. Experiments in Fluids, 57(10), 163.
Abstract
A free-surface synthetic Schlieren (Moisy et al. in Exp Fluids 46:1021–1036, 2009; Eddi et al. in J Fluid Mech 674:433–463, 2011) technique has been implemented in order to measure the surface topography generated by a droplet bouncing on a vibrating fluid bath. This method was used to capture the wave fields of bouncers, walkers, and walkers interacting with boundaries. These wave profiles are compared with existing theoretical models and simulations and will prove valuable in guiding their future development. Specifically, the method provides insight into what type of boundary conditions apply to the wave field when a bouncing droplet approaches a submerged obstacle.
Shedding light on pilot-wave phenomena
Brun, P. T., Harris, D. M., Prost, V., Quintela, J., & Bush, J. W. (2016). Shedding light on pilot-wave phenomena. Physical Review Fluids, 1(5), 050510.
ABSTRACT
This paper is associated with a video winner of a 2015 APS/DFD Gallery of Fluid Motion Award. The original video is available from the Gallery of Fluid Motion,
http://dx.doi.org/10.1103/APS.DFD.2015.GFM.V0064
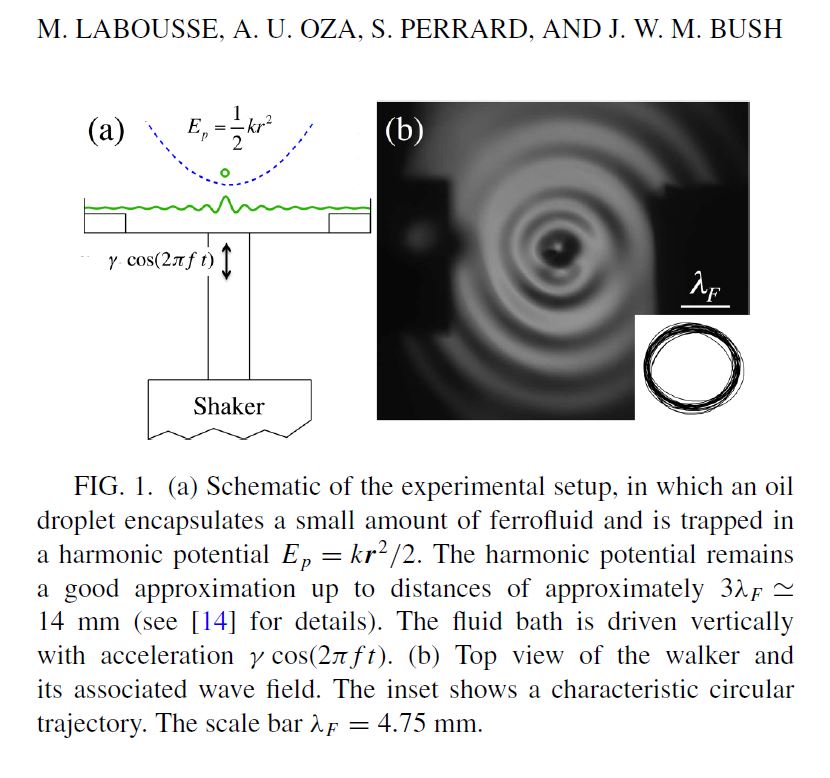
Pilot-wave dynamics in a harmonic potential : Quantization and stability of circular orbits
Labousse, M., Oza, A. U., Perrard, S., & Bush, J. W. (2016). Pilot-wave dynamics in a harmonic potential: Quantization and stability of circular orbits.Physical Review E, 93(3), 033122.
“We present the results of a theoretical investigation of the dynamics of a droplet walking on a vibrating fluid bath under the influence of a harmonic potential. The walking droplet’s horizontal motion is described by an integro-differential trajectory equation, which is found to admit steady orbital solutions. Predictions for the dependence of the orbital radius and frequency on the strength of the radial harmonic force field agree favorably with experimental data. The orbital quantization is rationalized through an analysis of the orbital solutions. The predicted dependence of the orbital stability on system parameters is compared with experimental data and the limitations of the model are discussed.”
Physics Today : letters to the editor
Some (heated ?) exchanges on the april edition of Physics today … with answers from John BUSH
Faraday pilot wave dynamics : modelling and computation
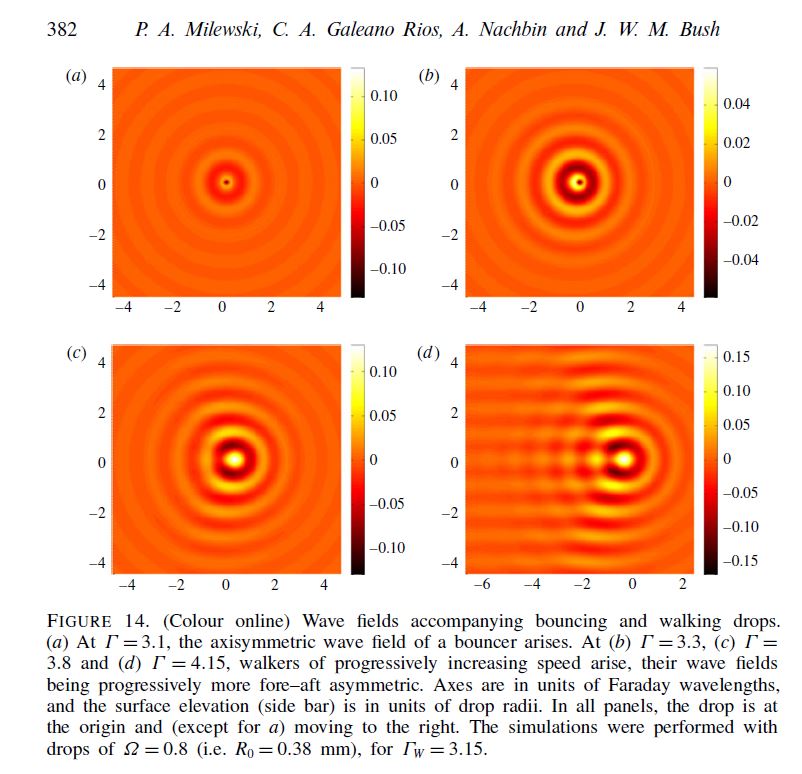
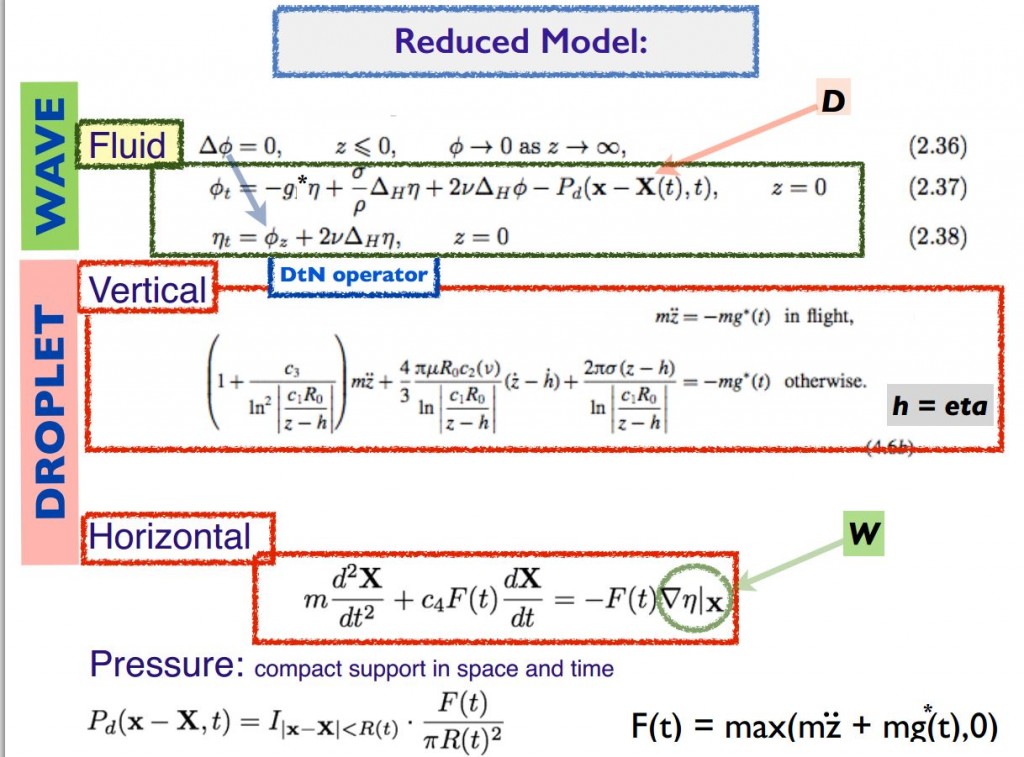
Milewski, P. A., Galeano-Rios, C. A., Nachbin, A., & Bush, J. W. (2015). Faraday pilot-wave dynamics: modelling and computation. Journal of Fluid Mechanics, 778, 361-388.
A millimetric droplet bouncing on the surface of a vibrating fluid bath can self-propel by virtue of a resonant interaction with its own wave field. This system represents the first known example of pilot-wave system of the form envisaged by Louis de Broglie in his double-solution pilot-wave theory. We here develop a fluid model of pilot-wave hydrodynamics by coupling recent models of the droplet’s bouncing dynamics with a more realistic model of weakly viscous quasi-potential wave generation and evolution. The resulting model is the first to capture a number of features reported in experiment, including the rapid transient wave generated during impact, the Doppler effect and walker–walker interactions.
Pilot-Wave Hydrodynamics (Annual Review of Fluid Mechanics 2015)
Bush, J. W. (2015). Pilot-wave hydrodynamics. Annual Review of Fluid Mechanics, 47, 269-292.
Yves Couder, Emmanuel Fort, and coworkers recently discovered that a millimetric droplet sustained on the surface of a vibrating fluid bath may self-propel through a resonant interaction with its own wave field. This article reviews experimental evidence indicating that the walking droplets exhibit certain features previously thought to be exclusive to the microscopic, quantum realm. It then reviews theoretical descriptions of this hydrodynamic pilot-wave system that yield insight into the origins of its quantumlike behavior. Quantization arises from the dynamic constraint imposed on the droplet by its pilot-wave field, and multimodal statistics appear to be a feature of chaotic pilot-wave dynamics. I attempt to assess the potential and limitations of this hydrodynamic system as a quantum analog. This fluid system is compared to quantum pilot-wave theories, shown to be markedly different from Bohmian mechanics and more closely related to de Broglie’s original conception of quantum dynamics, his double-solution theory, and its relatively recent extensions through researchers in stochastic electrodynamics.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2015/01/Bush-AnnRev2015.pdf
The wave-induced added mass of walking droplets
Bush, J. W., Oza, A. U., & Moláček, J. (2014). The wave-induced added mass of walking droplets. Journal of Fluid Mechanics, 755, R7.
It has recently been demonstrated that droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic realm. The walker, consisting of a droplet plus its guiding wavefield, is a spatially extended object. We here examine the dependence of the walker mass and momentum on its velocity. Doing so indicates that, when the walker’s time scale of acceleration is long relative to the wave decay time, its dynamics may be described in terms of the mechanics of a particle with a speed-dependent mass and a nonlinear drag force that drives it towards a fixed speed. Drawing an analogy with relativistic mechanics, we define a hydrodynamic boost factor for the walkers. This perspective provides a new rationale for the anomalous orbital radii reported in recent studies
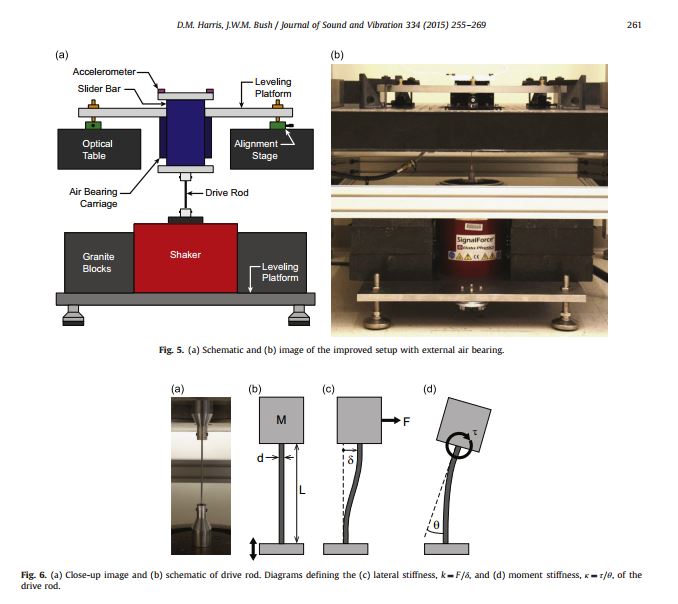
Generating uniaxial vibration with an electrodynamic shaker and external air bearing
Harris, D. M., & Bush, J. W. (2015). Generating uniaxial vibration with an electrodynamic shaker and external air bearing. Journal of Sound and Vibration,334, 255-269.
Electrodynamic shakers are widely used in experimental investigations of vibrated fluids and granular materials. However, they are plagued by undesirable internal resonances that can significantly impact the quality of vibration. In this work, we measure the performance of a typical shaker and characterize the influence that a payload has on its performance. We present the details of an improved vibration system based on a concept developed by Goldman (2002) [1] which consists of a typical electrodynamic shaker with an external linear air bearing to more effectively constrain the vibration to a single axis. The principal components and design criteria for such a system are discussed. Measurements characterizing the performance of the system demonstrate considerable improvement over the unmodified test shaker. In particular, the maximum inhomogeneity of the vertical vibration amplitude is reduced from approximately 10 percent to 0.1 percent; moreover, transverse vibrations were effectively eliminated.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2015/01/Harris-Shaker.pdf
A low‑cost, precise piezoelectric droplet‑on‑demand generator
Harris, D. M., Liu, T., & Bush, J. W. (2015). A low-cost, precise piezoelectric droplet-on-demand generator. Experiments in Fluids, 56(4), 1-7.
We present the design of a piezoelectric droplet-on-demand generator capable of producing droplets of highly repeatable size ranging from 0.5 to 1.4 mm in diameter. The generator is low cost and simple to fabricate. We demonstrate the manner in which droplet diameter can be controlled through variation of the piezoelectric driving waveform parameters, outlet pressure, and nozzle diameter.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2015/04/Harris-DropGenerator.pdf
Video Lesson – 07/06/2013 – Hydrodynamic Modelling of Pilot-Wave and boucing droplet coupling in a Faraday Problem
“Recent experiments by two groups, Yves Couder (Paris) and John
Bush (MIT) have shown experimentally that droplets will bounce on the
surface of a vertically vibrated bath (instead of coalescing with it),
generating a Faraday-type wavefield at every bounce. From this state, a
pitchfork symmetry breaking bifurcation leads to a “walking” state whereby
the bouncing droplet is “guided” by the self-generated wavefield – the
droplet’s pilot wave. Once this state is achieved a large array of
interesting dynamics ensues with surprising analogies to quantum
mechanical behaviour. We will present a coupled particle-fluid model that
can can be used simulate the dynamics of this problem. This is joint work
with John Bush, Andre Nachbin (IMPA) and Carlos Galeano (IMPA)”
Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization
Oza, A. U., Harris, D. M., Rosales, R. R., & Bush, J. W. (2014). Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization. Journal of Fluid Mechanics, 744, 404-429.
We present the results of a theoretical investigation of droplets walking on a
rotating vibrating fluid bath. The droplet’s trajectory is described in terms of an
integro-differential equation that incorporates the influence of its propulsive wave
force. Predictions for the dependence of the orbital radius on the bath’s rotation
rate compare favourably with experimental data and capture the progression from
continuous to quantized orbits as the vibrational acceleration is increased. The orbital
quantization is rationalized by assessing the stability of the orbital solutions, and may
be understood as resulting directly from the dynamic constraint imposed on the drop
by its monochromatic guiding wave. The stability analysis also predicts the existence
of wobbling orbital states reported in recent experiments, and the absence of stable
orbits in the limit of large vibrational forcing
A Hydrodynamic Pilot Wave Model : RIO 2014
Analysis of currrent state of the art modelling
Reflexions in a 1D Cavity
Computer simulations
(proceedings of RIO 2014 workshop)
http://www.personal.psu.edu/alm24/IMPA/talks/IMPANachbin.pdf
Droplets walking in a rotating frame: from quantized orbits to multimodal statistics
Harris, D. M., & Bush, J. W. (2014). Droplets walking in a rotating frame: from quantized orbits to multimodal statistics. Journal of Fluid Mechanics, 739, 444-464.
We present the results of an experimental investigation of a droplet walking on the
surface of a vibrating rotating fluid bath. Particular attention is given to demonstrating
that the stable quantized orbits reported by Fort et al. (Proc. Natl Acad. Sci.,
vol. 107, 2010, pp. 17515–17520) arise only for a finite range of vibrational
forcing, above which complex trajectories with multimodal statistics arise. We first
present a detailed characterization of the emergence of orbital quantization, and
then examine the system behaviour at higher driving amplitudes. As the vibrational
forcing is increased progressively, stable circular orbits are succeeded by wobbling
orbits with, in turn, stationary and drifting orbital centres. Subsequently, there is a
transition to wobble-and-leap dynamics, in which wobbling of increasing amplitude
about a stationary centre is punctuated by the orbital centre leaping approximately
half a Faraday wavelength. Finally, in the limit of high vibrational forcing, irregular
trajectories emerge, characterized by a multimodal probability distribution that reflects
the persistent dynamic influence of the unstable orbital states.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2014/01/HB-JFM-2014.pdf
A trajectory equation for walking droplets: hydrodynamic pilot-wave theory
Oza, A. U., Rosales, R. R., & Bush, J. W. (2013). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. Journal of Fluid Mechanics,737, 552-570.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/12/ORB-JFM.pdf
Integro-differential equation describing the horizontal motion of a walking droplet
Stability to perturbations
Drops bouncing on a vibrating bath
Moláček, J., & Bush, J. W. (2013). Drops bouncing on a vibrating bath. Journal of Fluid Mechanics, 727, 582-611.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB1-2013.pdf
Linear and logarithmic spring model of a boucing droplet