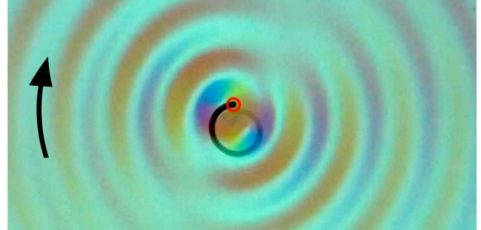
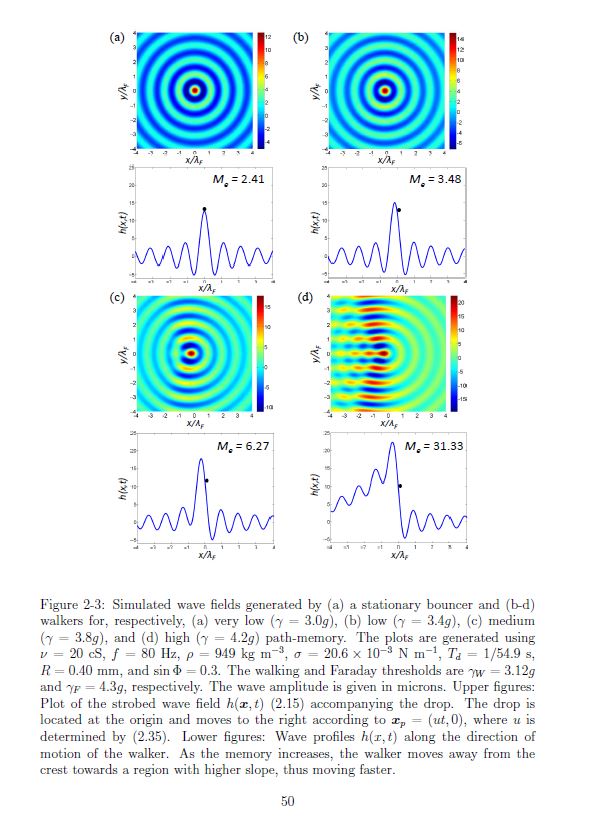
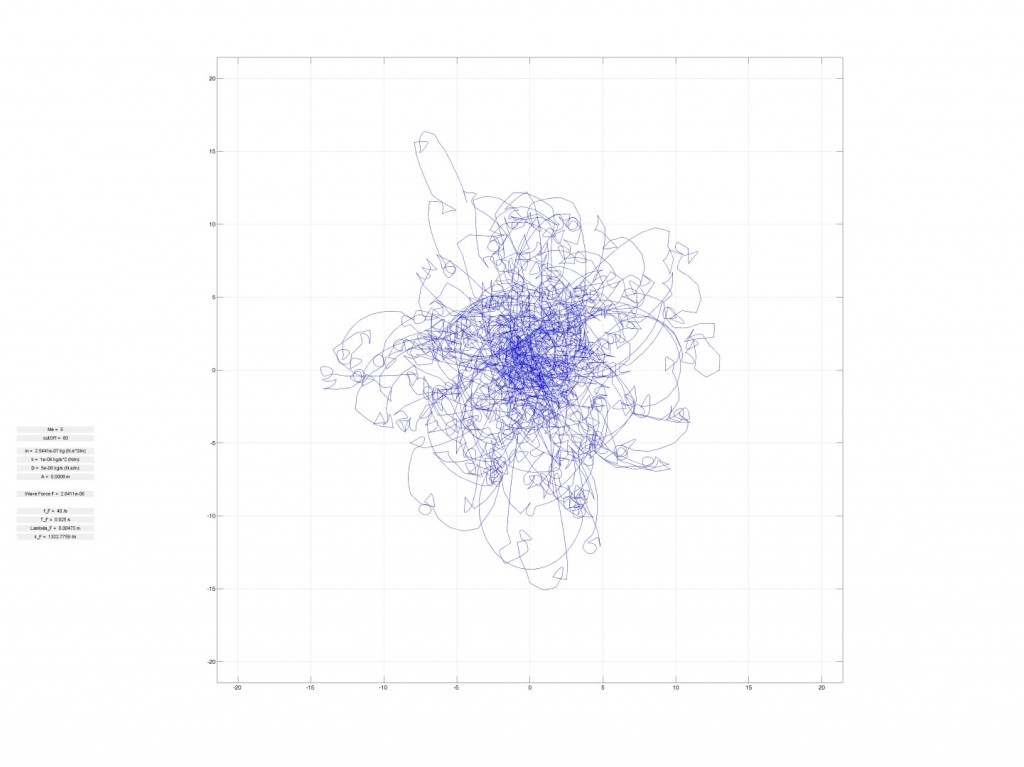
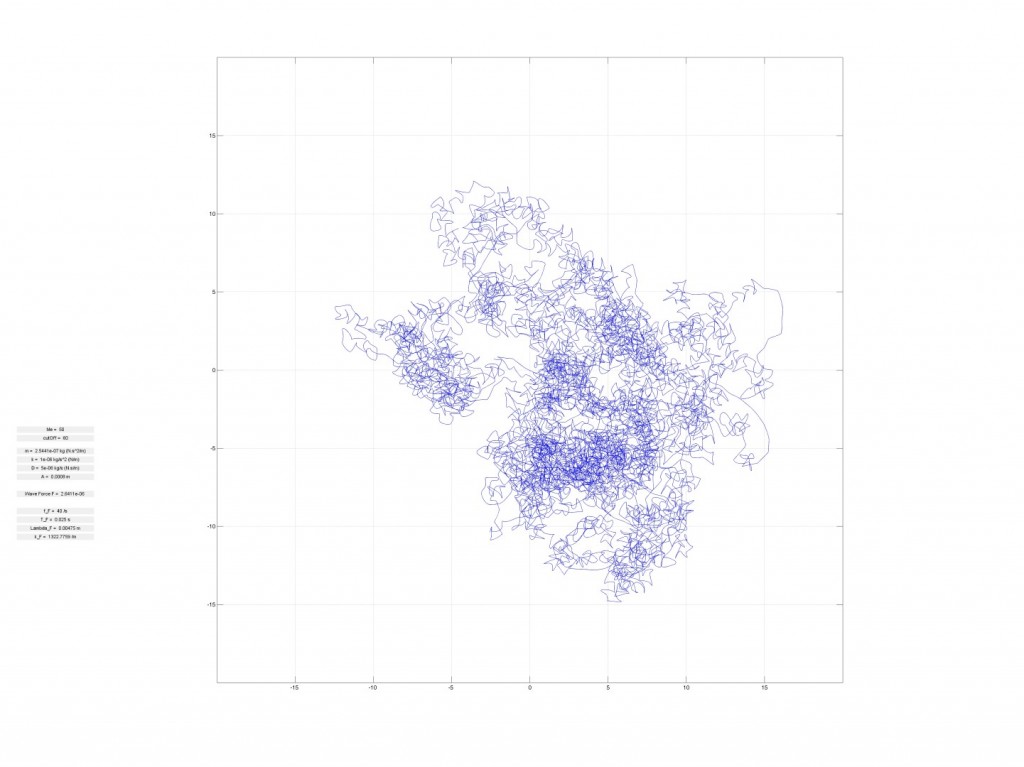
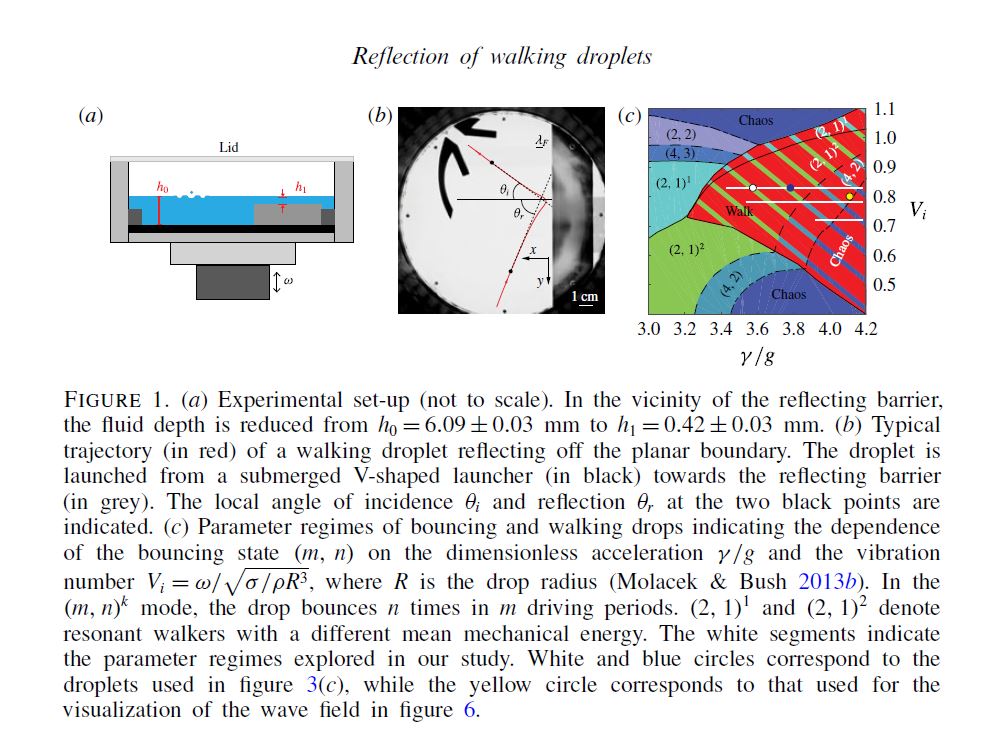
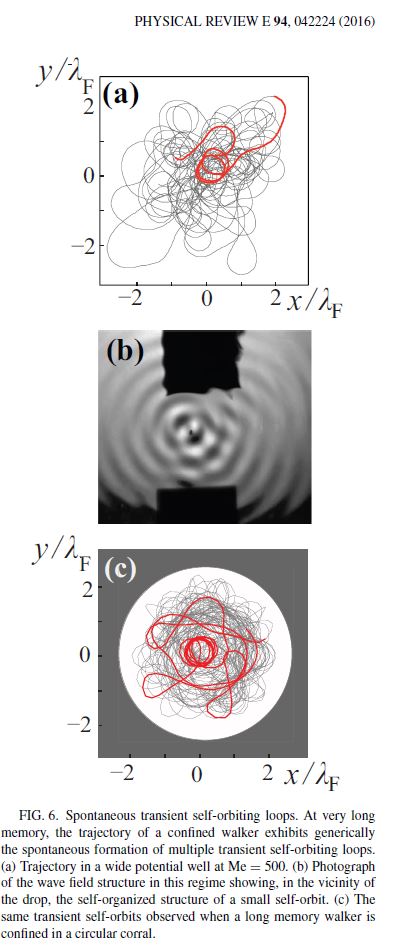
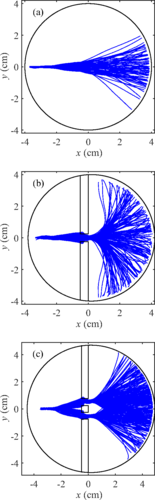
Is it possible for a free particle to spontaneously start spinning around a point without anything in the center of its path? The answer is yes.

Researchers at the Langevin Institute have just shown that a drop bouncing on a vertically vibrating liquid bath could remain captive to the waves it emitted during these successive bounces on the bath’s surface (see video). As in a kind of wave ballet, the drops first become walkers, propelled on the surface of the bath by the waves they emitted during their previous bounces. Then, spontaneously, they start to turn according to well-defined orbits, maintained in this perpetual movement by their past waves. It is in a way a “wave memory” that maintains them. The spontaneous emergence of a “spin” originates from the presence of a time-varying medium, the vibrating bath, which allows the emitted waves to be turned back in time and refocused on the source that initially produced them. Time-varying media are fascinating because they allow a source to be given a spatio-temporal non-locality, or more simply, to be clothed with a constantly changing past that determines its future.

Bernard-Bernardet, S., Fleury, M., & Fort, E. (2022). Spontaneous emergence of a spin state for an emitter in a time-varying medium. The European Physical Journal Plus, 137(4), 1-8.

ABSTRACT :

“Millimetric liquid droplets can walk across the surface of a vibrating fluid bath, self-propelled through a resonant interaction with their own guiding or ‘pilot’ wave fields. These walking droplets, or ‘walkers’, exhibit several features previously thought to be peculiar to the microscopic, quantum realm. In particular, walkers confined to circular corrals manifest a wave-like statistical behaviour reminiscent of that of electrons in quantum corrals. Here we demonstrate that localized topological inhomogeneities in an elliptical corral may lead to resonant projection effects in the walker’s statistics similar to those reported in quantum corrals. Specifically, we show that a submerged circular well may drive the walker to excite specific eigenmodes in the bath that result in drastic changes in the particle’s statistical behaviour. The well tends to attract the walker, leading to a local peak in the walker’s position histogram. By placing the well at one of the foci, a mode with maxima near the foci is preferentially excited, leading to a projection effect in the walker’s position histogram towards the empty focus, an effect strongly reminiscent of the quantum mirage. Finally, we demonstrate that the mean pilot-wave field has the same form as the histogram describing the walker’s statistics.”

Sáenz, P. J., Cristea-Platon, T., & Bush, J. W. (2018). Statistical projection effects in a hydrodynamic pilot-wave system. Nature Physics, 14(3), 315.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2017/12/Saenz-NatPhys-2017-.pdf

An interesting article from Tomas Bohr…the grandson of Niels Bohr !

“The walking droplets closely resemble quantum particles driven by a ‘pilot wave’, but how far the analogy can be taken is presently unknown”

Bohr, T. (2017). Quantum physics dropwise. Nature Physics, 1

http://fermatslibrary.com/s/quantum-physics-dropwise

See you in London next week ??

🙂

PhD Thesis : “In this work, we focus on a droplet, that can bounce on a liquid surface. More surprisingly this droplet can even move along a liquid surface. It is propelled by its own waves, generated at each bounce, and evolves at a well defined speed. This curious macroscopic object is called a « walker ». Moreover, it seems to present various analogies with the world of quantum mechanics and it has fascinated the scientists since its discovery in 2005 [34]. Indeed, the droplet is associated with its own waves, such that the droplet behaviour is intimately linked to the waves, which is a striking curiosity. In this thesis, we investigate further this subject of a droplet between wave-particle physics and fluid mechanics. Various experiments have been performed for a better understanding of walkers. They cover a wide range of 2d systems [35]. Some experiments develop methods to confine or trap droplets, upon using 2d harmonic potential (…)
However, there are only a few studies reported on a 1d system droplet. We wonder then, how to confine a droplet in 1d. Can we find a method to constrain its trajectory along a 1d path? Can experiments of walkers in 1d open new doors through other curiosities related to quantum mechanics? If not, how close to the wave-particle physics can we go? Is the walker entity a real analog to the quantum world, or just a curiosity ? As a starting point, we study the influence of the liquid height on the droplet behaviour. We wonder then how a linear cavity can trap a drop, and how the width of this cavity influences the confinement of a drop. How does droplet confinement affect the interactions between walkers? In this manuscript, we give answers to those different questions, and shed light on other curiosities.”

Proposition of an interferometer for walkers !

Filoux, B (2017), Walking droplet above cavities, Thèse, GRASP, Univ. Liège

orbi.ulg.be/bitstream/2268/214607/1/Thesis_BFiloux_WDAC.pdf

ABSTRACT : “A droplet may ‘walk’ across the surface of a vertically vibrating bath of the same fluid, due to the propulsive interaction with its wave field. This hydrodynamic pilotwave system exhibits many dynamics previously believed to exist only in the quantum realm. Starting from first principles, we derive a discrete-time fluid model, whereby the bath–droplet interactions are modelled as instantaneous. By analysing the stability of the fixed points of the system, we explain the dynamics of a walking droplet and capture the quantisations for multiple-droplet interactions. Circular orbits in a harmonic potential are studied, and a double quantisation of chaotic trajectories is obtained through systematic statistical analysis.”

Durey, M., & Milewski, P. A. (2017). Faraday wave–droplet dynamics: discrete-time analysis. Journal of Fluid Mechanics, 821, 296-329.

https://www.researchgate.net/

ABSTRACT : “Eddi et al. [Phys. Rev Lett. 102, 240401 (2009)] presented experimental results demonstrating the unpredictable tunneling of a classical wave-particle association as may arise when a droplet walking across the surface of a vibrating fluid bath approaches a submerged barrier.We here present a theoreticalmodel that captures the influence of bottom topography on this wave-particle association and so enables us to investigate its interaction 2 with barriers. The coupledwave-droplet dynamics results in unpredictable tunneling events.
As reported in the experiments by Eddi et al. and as is the case in quantum tunneling [Gamow, Nature (London) 122, 805 (1928)], the predicted tunneling probability decreases exponentially with increasing barrier width. In the parameter regimes examined, tunnelingbetween two cavities suggests an underlying stationary ergodic process for the droplet’s position.”

Nachbin, A., Milewski, P. A., & Bush, J. W. (2017). Tunneling with a hydrodynamic pilot-wave model. Physical Review Fluids, 2(3), 034801

Click to access NachbinMilewskiBush_PRF17.pdf

ABSTRACT : “When a droplet is placed onto a vertically vibrated bath, it can bouncewithout coalescing. Upon an increase of the forcing acceleration, the droplet is propelled by the wave it generates and becomes a walker with a well-defined speed.We investigate the confinement of a walker in different rectangular cavities, used as waveguides for the Faraday waves emitted by successive droplet bounces. By studying the walker velocities, we discover that one-dimensional confinement is optimal for narrow channels of width of D  1.5λF . Thereby, the walker follows a quasilinear path.We also propose an analogy with waveguide models based on the observation of the Faraday instability within the channels.”

Filoux, B., Hubert, M., Schlagheck, P., & Vandewalle, N. (2017). Walking droplets in linear channels. Physical Review Fluids, 2(1), 013601.

https://www.researchgate.net/publication/312353846_Walking_droplets_in_linear_channels

ABSTRACT : “We investigate the crossing of an energy barrier by a self-propelled particle described by a Rayleigh friction term. We show that a sharp transition between low and large amplitude of the external force field occurs. It corresponds to a saddle point transition in the velocity flow phase space, and would therefore occur for any type of force field. We use this approach to describe the results obtained by Eddi et al. [Phys. Rev. Lett. 102, 240401 (2009)] in 2009 who studied the interaction between a drop propelled by its own generated wave field and a submarine obstacle. It has been shown that this wave particle entity can overcome barrier of potential, suggesting the existence of a ”macroscopic tunnel effect”. We show that the effect of self-propulsion is sufficiently enough to generate crossing of high energy barrier. By assuming a random distribution of initial angles, we define a probability to cross the barrier of potential that matches with the data obtained by Eddi et al.. This probability appears similar to the one encountered in statistical physics for Hamiltonian systems i.e. a Boltzmann exponential law.”

Hubert, M., Labousse, M., & Perrard, S. (2017). Self-propulsion with random initial conditions: how to cross an energy barrier?. arXiv preprint arXiv:1701.01937.

Click to access 1701.01937.pdf

https://www.researchgate.nethttps://www.researchgate.net/profile/Matthieu_Labousse/publication/317945959_Self-propulsion_and_crossing_statistics_under_random_initial_conditions/links/59632e4f458515a3575449d5/Self-propulsion-and-crossing-statistics-under-random-initial-conditions.pdf

ABSTRACT  : “Yves Couder and coworkers have demonstrated that millimetric droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic quantum realm, including single-particle diffraction, tunneling, quantized orbits, and wave-like statistics in a corral. We here develop an integro-differential trajectory equation for these walking droplets with a view to gaining insight into their subtle dynamics. The orbital quantization is rationalized by assessing the stability of the orbital solutions. The stability analysis also predicts the existence of wobbling orbital states reported in recent experiments, and the absence of stable orbits in the limit of large vibrational forcing. In this limit, the complex walker dynamics give rise to a coherent statistical behavior with wave-like features. We characterize the progression from quantized orbits to chaotic dynamics as the vibrational forcing is increased progressively. We then describe the dynamics of a weakly-accelerating walker in terms of its wave-induced added mass, which provides rationale for the anomalously large orbital radii observed in experiments.”

Oza, A. U. (2014). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory (Doctoral dissertation, Massachusetts Institute of Technology).

https://dspace.mit.edu/bitstream/handle/1721.1/90191/890211673-MIT.pdf?sequence=2

These are trajectories of a dotwave in a central harmonic potential

Both trajectories have same parameters, only the memory of the bath differs.

Memory = 5

Memory = 50

Abstract : Couder et al. (Nature, vol. 437 (7056), 2005, p. 208) discovered that droplets walking on a vibrating bath possess certain features previously thought to be exclusive to quantum systems. These millimetric droplets synchronize with their Faraday wavefield, creating a macroscopic pilot-wave system. In this paper we exploit the fact that the waves generated are nearly monochromatic and propose a hydrodynamic model capable of quantitatively capturing the interaction between bouncing drops and a variable topography. We show that our reduced model is able to reproduce some important experiments involving the drop–topography interaction, such as non-specular reflection and single-slit diffraction.

Faria, L. M. (2017). A model for Faraday pilot waves over variable topography. Journal of Fluid Mechanics, 811, 51-66.

https://www.cambridge.org/

Abstract : Since their discovery by Yves Couder and Emmanuel Fort, droplets walking on a vibrating liquid bath have attracted considerable attention because they unexpectedly exhibit certain features reminiscent of quantum particles. While the behaviour of walking droplets in unbounded geometries has to a large extent been rationalized theoretically, no such rationale exists for their behaviour in the presence of boundaries, as arises in a number of key quantum analogue systems. We here present the results of a combined experimental and theoretical study of the interaction of walking droplets with a submerged planar barrier. Droplets exhibit non-specular reflection, with a small range of reflection angles that is only weakly dependent on the system parameters, including the angle of incidence. The observed behaviour is captured by simulations based on a theoretical model that treats the boundaries as regions of reduced wave speed, and rationalized in terms of momentum considerations.

Pucci, G., Sáenz, P. J., Faria, L. M., & Bush, J. W. (2016). Non-specular reflection of walking droplets. J Fluid Mech, 804, R3.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2016/09/Pucci-JFM-2016.pdf

Abstract : The back-reaction of a radiated wave on the emitting source is a general problem. In the most general case, back-reaction on moving wave sources depends on their whole history. Here we study a model system in which a pointlike source is piloted by its own memory-endowed wave field. Such a situation is implemented experimentally using a self-propelled droplet bouncing on a vertically vibrated liquid bath and driven by the waves it generates along its trajectory. The droplet and its associated wave field form an entity having an intrinsic dual particle-wave character. The wave field encodes in its interference structure the past trajectory of the droplet. In the present article we show that this object can self-organize into a spinning state in which the droplet possesses an orbiting motion without any external interaction. The rotation is driven by the wave-mediated attractive interaction of the droplet with its own past. The resulting “memory force” is investigated and characterized experimentally, numerically, and theoretically. Orbiting with a radius of curvature close to half a wavelength is shown to be a memory-induced dynamical attractor for the droplet’s motion.

Labousse, M., Perrard, S., Couder, Y., & Fort, E. (2016). Self-attraction into spinning eigenstates of a mobile wave source by its emission back-reaction. Physical Review E, 94(4), 042224.

Available on ResearchGate (Free login required)

Abstract  : We examine the orbital dynamics of droplets self-propelling along the surface of a vibrating bath. Circular orbital motion may arise when the walking droplet is subjected to one of three external force fields, the Coriolis force, a simple harmonic force, and a Coulomb force. Particular attention is given to a theoretical characterization of the onset of chaos that accompanies the destabilization of such circular orbits.

Tambasco, L., Harris, D., Oza, A., Rosales, R., & Bush, J. (2015, November). Onset of chaos in orbital pilot-wave dynamics. In APS Meeting Abstracts.

Paper available on researchgate.net/ (Requires free login)

A technical entry by the american team reproducing the synthetic Schlieren free surface measurment already implemented successfully by the Paris Team.

Damiano, A. P., Brun, P. T., Harris, D. M., Galeano-Rios, C. A., & Bush, J. W. (2016). Surface topography measurements of the bouncing droplet experiment. Experiments in Fluids, 57(10), 163.

Yet another report of failure in trying to reproduce the single particle slit diffraction experiment with walking droplets

Batelaan, H., Jones, E., Huang, W. C. W., & Bach, R. (2016). Momentum exchange in the electron double-slit experiment.

Abstract. We provide support for the claim that momentum is conserved for individual events in the electron double slit experiment. The natural consequence is that a physical mechanism is responsible for this momentum exchange, but that even if the fundamental mechanism is known for electron crystal diffraction and the Kapitza–Dirac effect, it is unknown for electron diffraction from nano-fabricated double slits. Work towards a proposed explanation in terms of particle trajectories affected by a vacuum field is discussed. The contentious use of trajectories is discussed within the context of oil droplet analogues of double slit diffraction.

http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1010&context=physicsbatelaan

Andersen, A., Madsen, J., Reichelt, C., Ahl, S. R., Lautrup, B., Ellegaard, C., … & Bohr, T. (2015). Double-slit experiment with single wave-driven particles and its relation to quantum mechanics. Physical Review E, 92(1), 013006.

ABSTRACT :

In a thought-provoking paper, Couder and Fort [Phys. Rev. Lett. 97, 154101 (2006)] describe a version of the famous double-slit experiment performed with droplets bouncing on a vertically vibrated fluid surface. In the experiment, an interference pattern in the single-particle statistics is found even though it is possible to determine unambiguously which slit the walking droplet passes. Here we argue, however, that the single-particle statistics in such an experiment will be fundamentally different from the single-particle statistics of quantum mechanics. Quantum mechanical interference takes place between different classical paths with precise amplitude and phase relations. In the double-slit experiment with walking droplets, these relations are lost since one of the paths is singled out by the droplet. To support our conclusions, we have carried out our own double-slit experiment, and our results, in particular the long and variable slit passage times of the droplets, cast strong doubt on the feasibility of the interference claimed by Couder and Fort. To understand theoretically the limitations of wave-driven particle systems as analogs to quantum mechanics, we introduce a Schrödinger equation with a source term originating from a localized particle that generates a wave while being simultaneously guided by it. We show that the ensuing particle-wave dynamics can capture some characteristics of quantum mechanics such as orbital quantization. However, the particle-wave dynamics can not reproduce quantum mechanics in general, and we show that the single-particle statistics for our model in a double-slit experiment with an additional splitter plate differs qualitatively from that of quantum mechanics.

http://sci-hub.bz/10.1103/physreve.92.013006#

The Paris team led by Yves Couder & Emmanuel Fort has published online a wonderful reference website, with many new videos

http://dualwalkers.com/