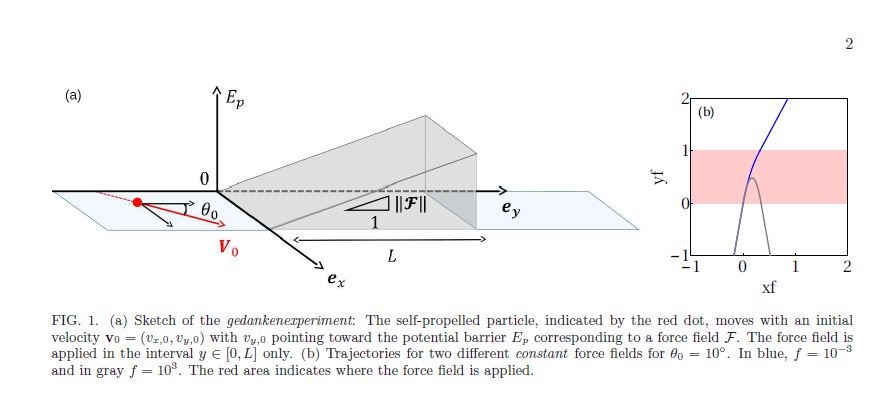
ABSTRACT : “We investigate the crossing of an energy barrier by a self-propelled particle described by a Rayleigh friction term. We show that a sharp transition between low and large amplitude of the external force field occurs. It corresponds to a saddle point transition in the velocity flow phase space, and would therefore occur for any type of force field. We use this approach to describe the results obtained by Eddi et al. [Phys. Rev. Lett. 102, 240401 (2009)] in 2009 who studied the interaction between a drop propelled by its own generated wave field and a submarine obstacle. It has been shown that this wave particle entity can overcome barrier of potential, suggesting the existence of a ”macroscopic tunnel effect”. We show that the effect of self-propulsion is sufficiently enough to generate crossing of high energy barrier. By assuming a random distribution of initial angles, we define a probability to cross the barrier of potential that matches with the data obtained by Eddi et al.. This probability appears similar to the one encountered in statistical physics for Hamiltonian systems i.e. a Boltzmann exponential law.”
Hubert, M., Labousse, M., & Perrard, S. (2017). Self-propulsion with random initial conditions: how to cross an energy barrier?. arXiv preprint arXiv:1701.01937.
Click to access 1701.01937.pdf