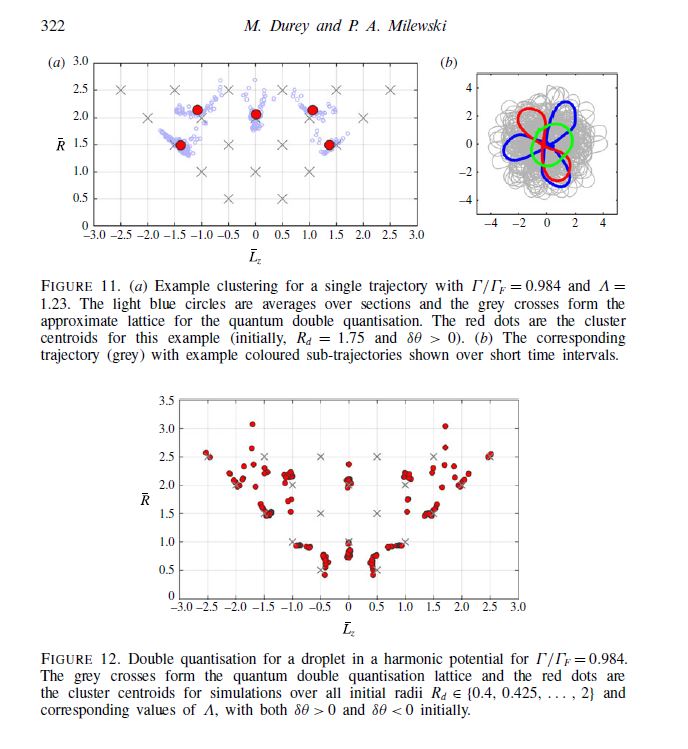
ABSTRACT : “A droplet may ‘walk’ across the surface of a vertically vibrating bath of the same fluid, due to the propulsive interaction with its wave field. This hydrodynamic pilotwave system exhibits many dynamics previously believed to exist only in the quantum realm. Starting from first principles, we derive a discrete-time fluid model, whereby the bath–droplet interactions are modelled as instantaneous. By analysing the stability of the fixed points of the system, we explain the dynamics of a walking droplet and capture the quantisations for multiple-droplet interactions. Circular orbits in a harmonic potential are studied, and a double quantisation of chaotic trajectories is obtained through systematic statistical analysis.”

Durey, M., & Milewski, P. A. (2017). Faraday wave–droplet dynamics: discrete-time analysis. Journal of Fluid Mechanics, 821, 296-329.

https://www.researchgate.net/

ABSTRACT : “Eddi et al. [Phys. Rev Lett. 102, 240401 (2009)] presented experimental results demonstrating the unpredictable tunneling of a classical wave-particle association as may arise when a droplet walking across the surface of a vibrating fluid bath approaches a submerged barrier.We here present a theoreticalmodel that captures the influence of bottom topography on this wave-particle association and so enables us to investigate its interaction 2 with barriers. The coupledwave-droplet dynamics results in unpredictable tunneling events.
As reported in the experiments by Eddi et al. and as is the case in quantum tunneling [Gamow, Nature (London) 122, 805 (1928)], the predicted tunneling probability decreases exponentially with increasing barrier width. In the parameter regimes examined, tunnelingbetween two cavities suggests an underlying stationary ergodic process for the droplet’s position.”

Nachbin, A., Milewski, P. A., & Bush, J. W. (2017). Tunneling with a hydrodynamic pilot-wave model. Physical Review Fluids, 2(3), 034801

Click to access NachbinMilewskiBush_PRF17.pdf

ABSTRACT  : “Yves Couder and coworkers have demonstrated that millimetric droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic quantum realm, including single-particle diffraction, tunneling, quantized orbits, and wave-like statistics in a corral. We here develop an integro-differential trajectory equation for these walking droplets with a view to gaining insight into their subtle dynamics. The orbital quantization is rationalized by assessing the stability of the orbital solutions. The stability analysis also predicts the existence of wobbling orbital states reported in recent experiments, and the absence of stable orbits in the limit of large vibrational forcing. In this limit, the complex walker dynamics give rise to a coherent statistical behavior with wave-like features. We characterize the progression from quantized orbits to chaotic dynamics as the vibrational forcing is increased progressively. We then describe the dynamics of a weakly-accelerating walker in terms of its wave-induced added mass, which provides rationale for the anomalously large orbital radii observed in experiments.”

Oza, A. U. (2014). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory (Doctoral dissertation, Massachusetts Institute of Technology).

https://dspace.mit.edu/bitstream/handle/1721.1/90191/890211673-MIT.pdf?sequence=2

Abstract : Couder et al. (Nature, vol. 437 (7056), 2005, p. 208) discovered that droplets walking on a vibrating bath possess certain features previously thought to be exclusive to quantum systems. These millimetric droplets synchronize with their Faraday wavefield, creating a macroscopic pilot-wave system. In this paper we exploit the fact that the waves generated are nearly monochromatic and propose a hydrodynamic model capable of quantitatively capturing the interaction between bouncing drops and a variable topography. We show that our reduced model is able to reproduce some important experiments involving the drop–topography interaction, such as non-specular reflection and single-slit diffraction.

Faria, L. M. (2017). A model for Faraday pilot waves over variable topography. Journal of Fluid Mechanics, 811, 51-66.

https://www.cambridge.org/

Rahman, A., & Blackmore, D. (2015). Neimark–Sacker bifurcation and evidence of chaos in a discrete dynamical model of walkers. arXiv preprint arXiv:1507.08057.

ABSTRACT

Bouncing droplets on a vibrating fluid bath can exhibit wave-particle behavior, such as being propelled by interacting with its own wave field. These droplets seem to walk across the bath, and thus are dubbed walkers. Experiments have shown that walkers can exhibit exotic dynamical behavior indicative of chaos. While the integro-differential models developed for these systems agree well with the experiments, they are difficult to analyze mathematically. In recent years, simpler discrete dynamical models have been derived and studied numerically. The numerical simulations of these models show evidence of exotic dynamics such as period doubling bifurcations, Neimark–Sacker (N–S) bifurcations, and even chaos. For example, in [Gilet, PRE 2014], based on simulations Gilet conjectured the existence of a supercritical N-S bifurcation as the damping factor in his one-dimensional path model. We prove Gilet’s conjecture and more; in fact, both supercritical and subcritical (N-S) bifurcations are produced by separately varying the damping factor and wave-particle coupling for all eigenmode shapes. Then we compare our theoretical results with some previous and new numerical simulations, and find complete qualitative agreement. Furthermore, evidence of chaos is shown by numerically studying a global bifurcation.

http://arxiv.org/pdf/1507.08057

Dubertrand, R., Hubert, M., Schlagheck, P., Vandewalle, N., Bastin, T., & Martin, J. (2016). Scattering theory of walking droplets in the presence of obstacles. arXiv preprint arXiv:1605.02370.

We aim to describe a droplet bouncing on a vibrating bath. Due to Faraday instability a surface wave is created at each bounce and serves as a pilot wave of the droplet. This leads to so called walking droplets or walkers. Since the seminal experiment by Couder et al [Phys. Rev. Lett. 97, 154101 (2006)] there have been many attempts to accurately reproduce the experimental results. Here we present a simple and highly versatile model inspired from quantum mechanics. We propose to describe the trajectories of a walker using a Green function approach. The Green function is related to Helmholtz equation with Neumann boundary conditions on the
obstacle(s) and outgoing conditions at infinity. For a single slit geometry our model is exactly solvable and reproduces some general features observed experimentally. It
stands for a promising.

http://arxiv.org/pdf/1605.02370.pdf

Labousse, M., Oza, A. U., Perrard, S., & Bush, J. W. (2016). Pilot-wave dynamics in a harmonic potential: Quantization and stability of circular orbits.Physical Review E, 93(3), 033122.

“We present the results of a theoretical investigation of the dynamics of a droplet walking on a vibrating fluid bath under the influence of a harmonic potential. The walking droplet’s horizontal motion is described by an integro-differential trajectory equation, which is found to admit steady orbital solutions. Predictions for the dependence of the orbital radius and frequency on the strength of the radial harmonic force field agree favorably with experimental data. The orbital quantization is rationalized through an analysis of the orbital solutions. The predicted dependence of the orbital stability on system parameters is compared with experimental data and the limitations of the model are discussed.”

http://arxiv.org/pdf/1604.07394

Richardson, C. D., Schlagheck, P., Martin, J., Vandewalle, N., & Bastin, T. (2014). On the analogy of quantum wave-particle duality with bouncing droplets.arXiv preprint arXiv:1410.1373.

We explore the hydrodynamic analogues of quantum wave-particle duality in the context of a bouncing droplet system which we model in such a way as to promote comparisons to the de Broglie-Bohm interpretation of quantum mechanics. Through numerical means we obtain single-slit difraction and double-slit interference patterns that strongly resemble those reported in experiment and that re ect a striking resemblance to quantum diraction and interference on a phenomenological level. We, however, identify evident dierences from quantum mechanics which arise from the governing equations at the fundamental level.

http://arxiv.org/pdf/1410.1373.pdf

Labousse, M., Perrard, S., Couder, Y., & Fort, E. (2014). Build-up of macroscopic eigenstates in a memory-based constrained system. New Journal of Physics, 16(11), 113027.

A bouncing drop and its associated accompanying wave forms a walker. Based on previous works, we show in this article that it is possible to formulate a simple theoretical framework for the walker dynamics. It relies on a time scale decomposition corresponding to the effects successively generated when the memory effects increase. While the short time scale effect is simply responsible for the walkerʼs propulsion, the intermediate scale generates spontaneously pivotal structures endowed with angular momentum. At an even larger memory
scale, if the walker is spatially confined, the pivots become the building blocks of a self-organization into a global structure. This new theoretical framework is applied in the presence of an external harmonic potential, and reveals the underlying mechanisms leading to the emergence of the macroscopic spatial organization reported by Perrard et al (2014 Nature Commun. 5 3219).

https://hal-univ-artois.archives-ouvertes.fr/hal-01084731/document

Bush, J. W., Oza, A. U., & Moláček, J. (2014). The wave-induced added mass of walking droplets. Journal of Fluid Mechanics, 755, R7.

It has recently been demonstrated that droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic realm. The walker, consisting of a droplet plus its guiding wavefield, is a spatially extended object. We here examine the dependence of the walker mass and momentum on its velocity. Doing so indicates that, when the walker’s time scale of acceleration is long relative to the wave decay time, its dynamics may be described in terms of the mechanics of a particle with a speed-dependent mass and a nonlinear drag force that drives it towards a fixed speed. Drawing an analogy with relativistic mechanics, we define a hydrodynamic boost factor for the walkers. This perspective provides a new rationale for the anomalous orbital radii reported in recent studies

Click to access Boost-JFM.pdf

Grössing, G., Fussy, S., Pascasio, J. M., & Schwabl, H. (2014, April). Relational causality and classical probability: Grounding quantum phenomenology in a superclassical theory. In Journal of Physics: Conference Series (Vol. 504, No. 1, p. 012006). IOP Publishing.

Abstract. : By introducing the concepts of \superclassicality” and \relational causality”, it is shown here that the velocity eld emerging from an n-slit system can be calculated as an
average classical velocity eld with suitable weightings per channel. No deviation from classical probability theory is necessary in order to arrive at the resulting probability distributions.
In addition, we can directly show that when translating the thus obtained expression for said velocity eld into a more familiar quantum language, one immediately derives the basic
postulate of the de Broglie-Bohm theory, i.e. the guidance equation, and, as a corollary, the exact expression for the quantum mechanical probability density current. Some other direct
consequences of this result will be discussed, such as an explanation of Born’s rule and Sorkin’s first and higher order sum rules, respectively.

http://iopscience.iop.org/1742-6596/504/1/012006/pdf/1742-6596_504_1_012006.pdf

classical probability theory

n-slit system

guidance equation

Sbitnev, V. I. (2013). Droplets moving on a fluid surface: interference pattern from two slits. arXiv preprint arXiv:1307.6920.

http://arxiv.org/pdf/1307.6920.pdf

Feynman path integral approach

Droplet / Antidroplet

Soliton diffraction

Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of” hidden” variables. I. Physical Review, 85(2), 166.

http://www.psiquadrat.de/downloads/bohm52a.pdf

Hidden variable theory foundation

Moláček, J., & Bush, J. W. (2013). Drops bouncing on a vibrating bath. Journal of Fluid Mechanics, 727, 582-611.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB1-2013.pdf

Linear and logarithmic  spring model of a boucing droplet

Wind-Willassen, Ø., Moláček, J., Harris, D. M., & Bush, J. W. (2013). Exotic states of bouncing and walking droplets. Physics of Fluids, 25, 082002.

http://windw.dk/2013Bouncing.pdf

Phase diagram refinement : the different styles of bouncing

Moláček, J., & Bush, J. W. (2013). Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory. Journal of Fluid Mechanics, 727, 582-617.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB2-2013.pdf

The most advanced theoretical model

Oriols, X., & Mompart, J. (2012). Overview of Bohmian Mechanics. arXiv preprint arXiv:1206.1084.

http://arxiv.org/pdf/1206.1084.pdf

Overview of the guiding wave quantum physics theory, known as “Bohmian mechanics”