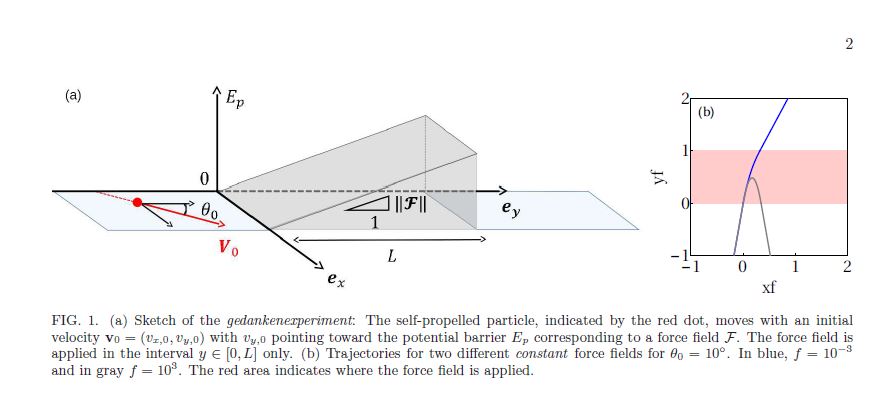
ABSTRACT : “We investigate the crossing of an energy barrier by a self-propelled particle described by a Rayleigh friction term. We show that a sharp transition between low and large amplitude of the external force field occurs. It corresponds to a saddle point transition in the velocity flow phase space, and would therefore occur for any type of force field. We use this approach to describe the results obtained by Eddi et al. [Phys. Rev. Lett. 102, 240401 (2009)] in 2009 who studied the interaction between a drop propelled by its own generated wave field and a submarine obstacle. It has been shown that this wave particle entity can overcome barrier of potential, suggesting the existence of a ”macroscopic tunnel effect”. We show that the effect of self-propulsion is sufficiently enough to generate crossing of high energy barrier. By assuming a random distribution of initial angles, we define a probability to cross the barrier of potential that matches with the data obtained by Eddi et al.. This probability appears similar to the one encountered in statistical physics for Hamiltonian systems i.e. a Boltzmann exponential law.”

Hubert, M., Labousse, M., & Perrard, S. (2017). Self-propulsion with random initial conditions: how to cross an energy barrier?. arXiv preprint arXiv:1701.01937.

Click to access 1701.01937.pdf

https://www.researchgate.nethttps://www.researchgate.net/profile/Matthieu_Labousse/publication/317945959_Self-propulsion_and_crossing_statistics_under_random_initial_conditions/links/59632e4f458515a3575449d5/Self-propulsion-and-crossing-statistics-under-random-initial-conditions.pdf

Abstract : The back-reaction of a radiated wave on the emitting source is a general problem. In the most general case, back-reaction on moving wave sources depends on their whole history. Here we study a model system in which a pointlike source is piloted by its own memory-endowed wave field. Such a situation is implemented experimentally using a self-propelled droplet bouncing on a vertically vibrated liquid bath and driven by the waves it generates along its trajectory. The droplet and its associated wave field form an entity having an intrinsic dual particle-wave character. The wave field encodes in its interference structure the past trajectory of the droplet. In the present article we show that this object can self-organize into a spinning state in which the droplet possesses an orbiting motion without any external interaction. The rotation is driven by the wave-mediated attractive interaction of the droplet with its own past. The resulting “memory force” is investigated and characterized experimentally, numerically, and theoretically. Orbiting with a radius of curvature close to half a wavelength is shown to be a memory-induced dynamical attractor for the droplet’s motion.

Labousse, M., Perrard, S., Couder, Y., & Fort, E. (2016). Self-attraction into spinning eigenstates of a mobile wave source by its emission back-reaction. Physical Review E, 94(4), 042224.

Available on ResearchGate (Free login required)

Labousse, M., Oza, A. U., Perrard, S., & Bush, J. W. (2016). Pilot-wave dynamics in a harmonic potential: Quantization and stability of circular orbits.Physical Review E, 93(3), 033122.

“We present the results of a theoretical investigation of the dynamics of a droplet walking on a vibrating fluid bath under the influence of a harmonic potential. The walking droplet’s horizontal motion is described by an integro-differential trajectory equation, which is found to admit steady orbital solutions. Predictions for the dependence of the orbital radius and frequency on the strength of the radial harmonic force field agree favorably with experimental data. The orbital quantization is rationalized through an analysis of the orbital solutions. The predicted dependence of the orbital stability on system parameters is compared with experimental data and the limitations of the model are discussed.”

http://arxiv.org/pdf/1604.07394

Bacot, V., Labousse, M., Eddi, A., Fink, M., & Fort, E. (2015). Revisiting time reversal and holography with spacetime transformations. arXiv preprint arXiv:1510.01277.

Wave control is usually performed by spatially engineering the properties of a medium. Because time and space play similar roles in wave propagation, manipulating time boundaries provides a complementary approach. Here, we experimentally demonstrate the relevance of this concept by introducing instantaneous time mirrors. We show with water waves that a sudden change of the effective gravity generates time-reversed waves that refocus at the source. We generalize this concept for all kinds of waves introducing a universal framework which explains the effect of any time disruption on wave propagation. We show that sudden changes of the medium properties generate instant wave sources that emerge instantaneously from the entire space at the time disruption. The time-reversed waves originate from these “Cauchy sources” which are the counterpart of Huygens virtual sources on a time boundary. It allows us to revisit the holographic method and introduce a new approach for wave control.

http://arxiv.org/ftp/arxiv/papers/1510/1510.01277.pdf

Borghesi, C., Moukhtar, J., Labousse, M., Eddi, A., Fort, E., & Couder, Y. (2014). Interaction of two walkers: Wave-mediated energy and force. Physical Review E, 90(6), 063017.

A bouncing droplet, self-propelled by its interaction with the waves it generates, forms a classical wave-particle association called a “walker.” Previous works have demonstrated that the dynamics of a single walker is driven by its global surface wave field that retains information on its past trajectory. Here, we investigate the energy stored in this wave field for two coupled walkers and how it conveys an interaction between them. For this purpose, we characterize experimentally the “promenade modes” where two walkers are bound, and propagate together. Their possible binding distances take discrete values, and the velocity of the pair depends on their mutual binding. The mean parallel motion can be either rectilinear or oscillating. The experimental results are recovered analytically with a simple theoretical framework. A relation between the kinetic energy of the droplets and the total energy of the standing waves is established.

http://arxiv.org/pdf/1412.7701.pdf

Labousse, M., Perrard, S., Couder, Y., & Fort, E. (2014). Build-up of macroscopic eigenstates in a memory-based constrained system. New Journal of Physics, 16(11), 113027.

A bouncing drop and its associated accompanying wave forms a walker. Based on previous works, we show in this article that it is possible to formulate a simple theoretical framework for the walker dynamics. It relies on a time scale decomposition corresponding to the effects successively generated when the memory effects increase. While the short time scale effect is simply responsible for the walkerʼs propulsion, the intermediate scale generates spontaneously pivotal structures endowed with angular momentum. At an even larger memory
scale, if the walker is spatially confined, the pivots become the building blocks of a self-organization into a global structure. This new theoretical framework is applied in the presence of an external harmonic potential, and reveals the underlying mechanisms leading to the emergence of the macroscopic spatial organization reported by Perrard et al (2014 Nature Commun. 5 3219).

https://hal-univ-artois.archives-ouvertes.fr/hal-01084731/document

Perrard, S., Labousse, M., Fort, E., & Couder, Y. (2014). Chaos driven by interfering memory. Physical review letters, 113(10), 104101.

The transmission of information can couple two entities of very different nature, one of them serving as a memory for the other. Here we study the situation in which information is stored in a wave field and serves as a memory that pilots the dynamics of a particle. Such a system can be implemented by a bouncing drop generating surface waves sustained by a parametric forcing. The motion of the resulting “walker” when confined in a harmonic potential well is generally disordered. Here we show that these trajectories correspond to chaotic regimes characterized by intermittent transitions between a discrete set of states. At any given time, the system is in one of these states characterized by a double quantization of size and angular momentum. A low dimensional intermittency determines their respective probabilities. They thus form an eigenstate basis of decomposition for what would be observed as a superposition of states if all measurements were intrusive

https://hal.archives-ouvertes.fr/hal-01061415/document

“À l’échelle macroscopique, les ondes et les particules sont des objets distincts. La découverte d’objets appelés marcheurs, constitués d’une goutte rebondissant sur un bain liquide vibré verticalement, a montré qu’il n’en était rien. La goutte est autopropulsée, guidée sur la surface du liquide par l’onde qu’elle a elle-même créée lors des rebonds précédents. Ces objets possèdent une dynamique originale dominée par le concept de mémoire de chemin. La structure du champ d’onde qui guide la goutte dépend, en effet, de la position des rebonds passés disposés le long de la trajectoire. La profondeur de cette mémoire peut, de plus, être contrôlée expérimentalement en changeant l’accélération du bain. De nombreuses réalisations expérimentales ont mis en évidence les comportements dynamiques singuliers de ces systèmes couplés goutte/onde. Cette thèse répond à la nécessité d’une compréhension théorique des effets non locaux en temps introduit par la mémoire de chemin. Pour ce faire, nous étudierons l’évolution d’un marcheur numérique en potentiel harmonique bidimensionnel. Un ensemble relativement restreint de trajectoires stables est obtenu. Nous constaterons que ces dernières sont quantifiées en extension moyenne et en moment angulaire moyen. Nous analyserons comment s’imbriquent les différentes échelles de temps de la dynamique, permettant ainsi de dissocier les termes propulsifs à temps court de l’émergence de structures ondulatoires cohérentes à temps long. Nous verrons en quoi l’expression du caractère non-local d’un marcheur permet d’en révéler les symétries internes et d’assurer la convergence du système dynamique vers un jeu d’états propres de basse dimension.”

Labousse, M. (2014). Étude d’une dynamique à mémoire de chemin: une expérimentation théorique (Doctoral dissertation, Université Pierre et Marie Curie UPMC Paris VI).

https://pastel.archives-ouvertes.fr/tel-01114815/document

Perrard, S., Labousse, M., Miskin, M., Fort, E., & Couder, Y. Effets de quantification d’une association onde-particule soumise à une force centrale.Résumés des exposés de la 16e Rencontre du Non-Linéaire Paris 2013, 68.

http://nonlineaire.univ-lille1.fr/SNL/media/2012/CR/Perrard.pdf

eigenstates in circular cavity