Spontaneous emergence of a spin state for an emitter in a time-varying medium

Is it possible for a free particle to spontaneously start spinning around a point without anything in the center of its path? The answer is yes.
Researchers at the Langevin Institute have just shown that a drop bouncing on a vertically vibrating liquid bath could remain captive to the waves it emitted during these successive bounces on the bath’s surface (see video). As in a kind of wave ballet, the drops first become walkers, propelled on the surface of the bath by the waves they emitted during their previous bounces. Then, spontaneously, they start to turn according to well-defined orbits, maintained in this perpetual movement by their past waves. It is in a way a “wave memory” that maintains them. The spontaneous emergence of a “spin” originates from the presence of a time-varying medium, the vibrating bath, which allows the emitted waves to be turned back in time and refocused on the source that initially produced them. Time-varying media are fascinating because they allow a source to be given a spatio-temporal non-locality, or more simply, to be clothed with a constantly changing past that determines its future.
Bernard-Bernardet, S., Fleury, M., & Fort, E. (2022). Spontaneous emergence of a spin state for an emitter in a time-varying medium. The European Physical Journal Plus, 137(4), 1-8.
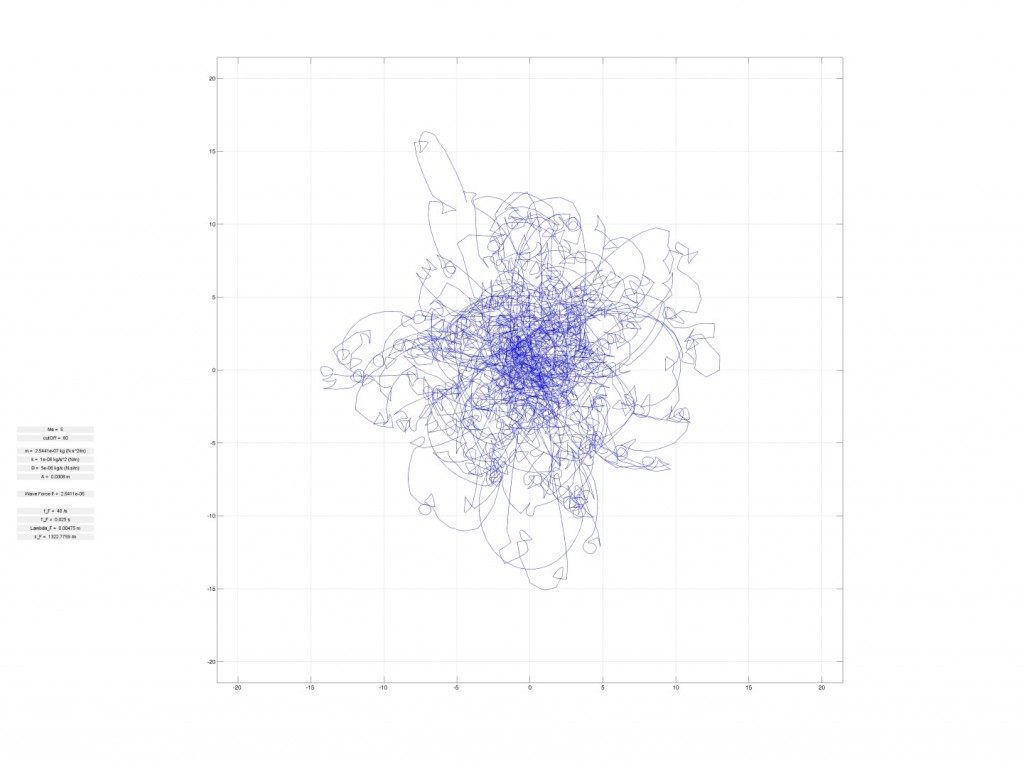
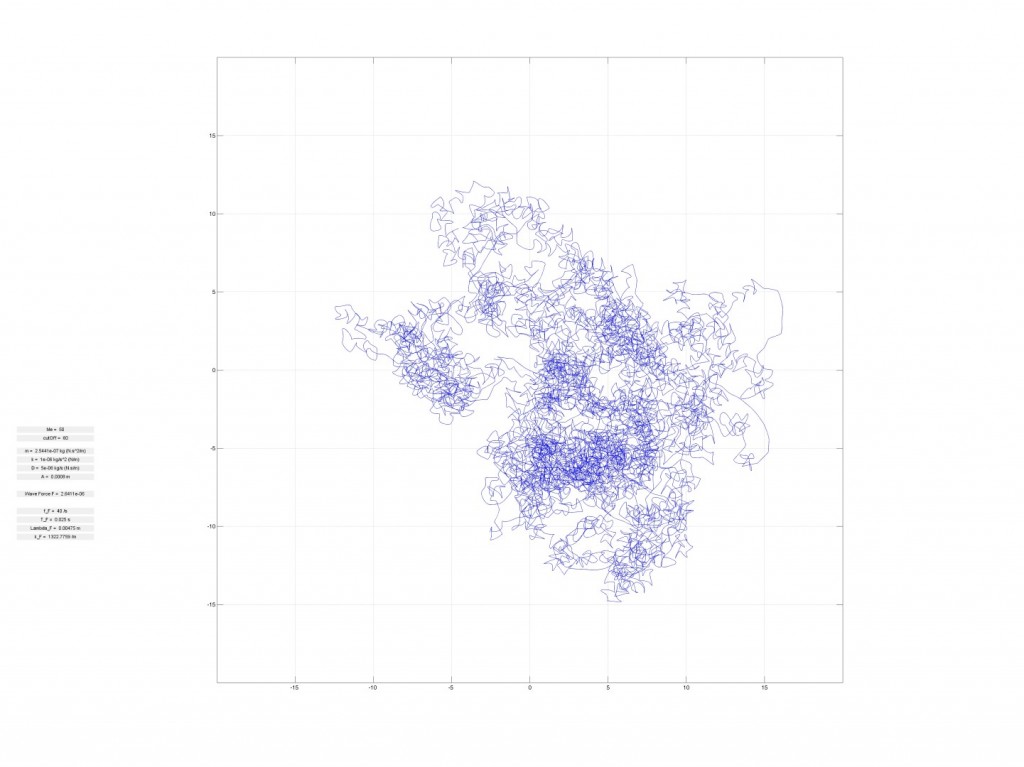
Influence of memory on trajectory in a harmonic potential
These are trajectories of a dotwave in a central harmonic potential
Both trajectories have same parameters, only the memory of the bath differs.
Memory = 5
New reference website from Paris Couder & Fort Team
The Paris team led by Yves Couder & Emmanuel Fort has published online a wonderful reference website, with many new videos
emergence of statistical pattern in a 1D cavity
On this video you will see how a walking droplet in a small 1D cavity moves “randomly” if the memory of the system is high enough (ie if the forcing is strong enough, but still below the Faraday Thresold)
And how a statistical pattern emerges with time
Rainbow colored dotwave
These pictures illustrate path memory : in the wake of the drop, there is a superposition of a circular wave due to latest impact and of “line waves” created by the many previous bounces
Dotwave picture on Phys.org
Russian Physicians from Moscow Institute of Physics and Technology have chosen a dotwave.org picture to illustrate an article published on phys.org concerning their latest paper,
Des physiciens russes de l’institut de physique et de technologie de Moscou ont choisi une de mes photos pour illustrer un résumé d’un de leur papier sur les ondes de Faraday publié sur phys.org
Physics Today : letters to the editor
Some (heated ?) exchanges on the april edition of Physics today … with answers from John BUSH
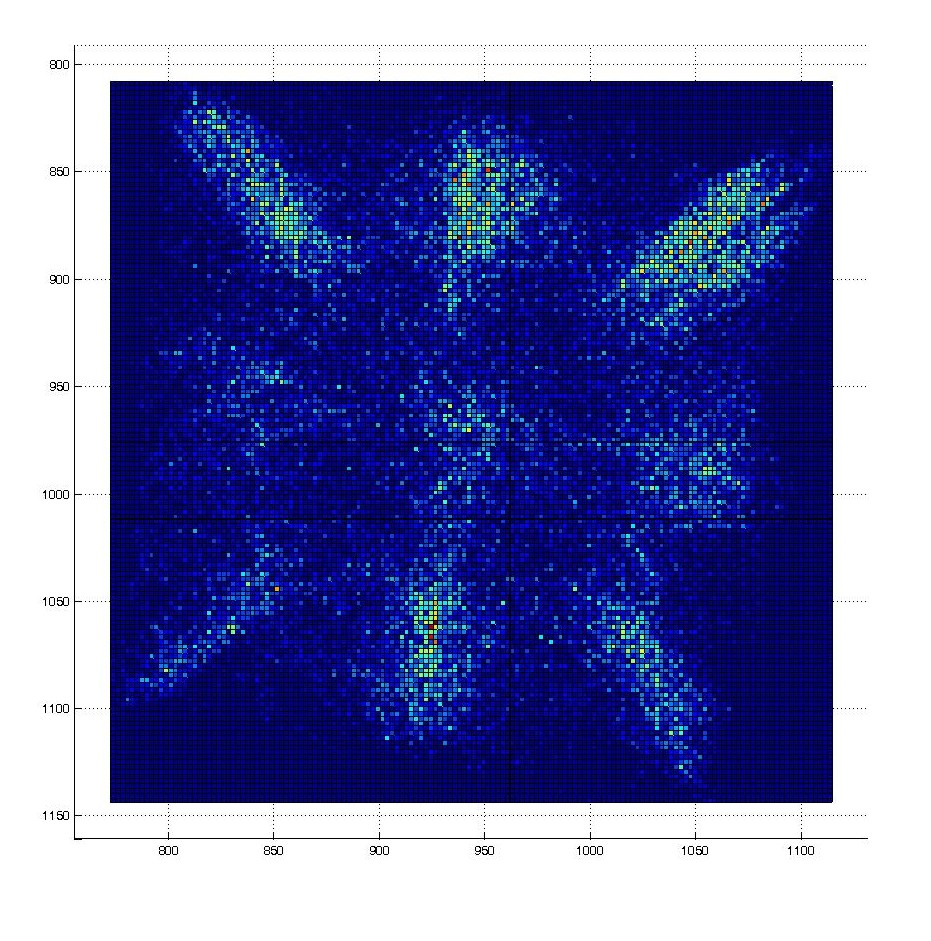
Emergent quantization in a square box
Goal of the experiment :
A walking droplet is placed in a square box, at the onset of Faraday thresold.
The trajectory of the droplet is mapped.
In the long time limit, does a self-interference pattern appear ? what’s its shape ? How does it relate to the square cavity surface wave eigen-modes ?
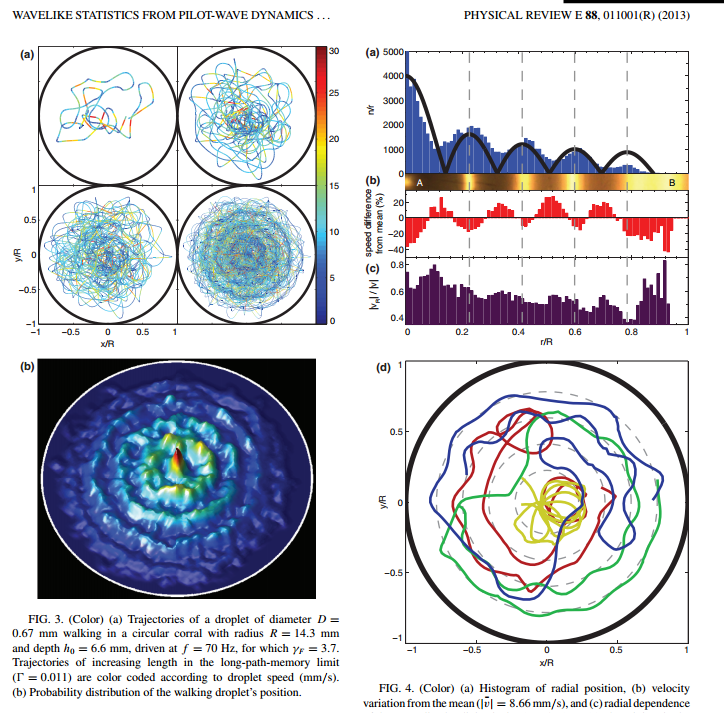
cf. experiment by Bush et al. : in a circular corral
http://dotwave.org/wavelike-statistics-from-pilot-wave-dynamics-in-a-circular-corral/
In short, we try to reproduce the experiment of Bush et al, but in a square box.
First result :
A walking droplet in a square cavity shows random motion, but with time, its trajectory is building a statistic reminiscent of the resonant mode of the cavity.
This can be seen by the naked eye in this movie excerpt :
This is then confirmed with optical tracking measurment of the trajectory :
The position distribution (~probability density) is then computed :
PDF Version of this résumé :
Emergent quantization of trajectories in a square box
Mini Colloque RNL 2016 : Dualité onde-corpuscule à l’échelle macroscopique
I was lucky enough to attend this mini-colloque !!
“Si la dualité onde-corpuscule est une des bases de l’interprétation de la mécanique quantique, elle peut aussi se manifester à l’échelle macroscopique. Durant ce mini-colloque seront présentées les propriétés observées dans des systèmes macroscopiques, ainsi que quelques-unes de leurs pendants aux échelles microscopiques. Un des objectifs est d’identifier les analogies et les différences entre ces deux types de systèmes.”
http://nonlineaire.univ-lille1.fr/SNL/media/2016/programme/ProgrammeMiniColloque2016.pdf
DotWave Keynote at XLIM Lab in Limoges
A live demonstration with a brief theoretical introduction to walking droplets and their wonders was held successfully at XLIM labs in Limoges last week.
50 attendees, mainly professionnal researchers in the field of photonics and microwave and their PhD student.
“Fingers and Holes in a Shaken Cornstrach Solution” sur YouTube
Quasi particles in the middle of faraday waves :
Fingers and Holes in a Shaken Cornstrach Solution : http://youtu.be/DrcShENMaoI
Video Lesson – 07/06/2013 – Hydrodynamic Modelling of Pilot-Wave and boucing droplet coupling in a Faraday Problem
“Recent experiments by two groups, Yves Couder (Paris) and John
Bush (MIT) have shown experimentally that droplets will bounce on the
surface of a vertically vibrated bath (instead of coalescing with it),
generating a Faraday-type wavefield at every bounce. From this state, a
pitchfork symmetry breaking bifurcation leads to a “walking” state whereby
the bouncing droplet is “guided” by the self-generated wavefield – the
droplet’s pilot wave. Once this state is achieved a large array of
interesting dynamics ensues with surprising analogies to quantum
mechanical behaviour. We will present a coupled particle-fluid model that
can can be used simulate the dynamics of this problem. This is joint work
with John Bush, Andre Nachbin (IMPA) and Carlos Galeano (IMPA)”
SPH Simulation of a walking droplet
A new kind of simulation using Smoothed particle hydrodynamics by Diego Molteni, Università degli studi di Palermo, Dipartimento di Fisica e Chimic
Vortex-mediated bouncing drops on an oscillating liquid
Chu, H. Y., & Fei, H. T. (2014). Vortex-mediated bouncing drops on an oscillating liquid. Physical Review E, 89(6), 063011
http://journals.aps.org/pre/abstract/10.1103/PhysRevE.89.063011 (Subsrciption required)
Stunning Vizualisization of undersurface flows
Abstract :
We have investigated the behavior of bouncing drops on a liquid surface by using particle image velocimetry analysis. A drop on an oscillating liquid surface is observed to not coalesce with the liquid and to travel along the surface if the oscillation is strong enough. A streaming vortex pair, induced by the alternatively distorted liquid surface, shows up below a bouncing drop. The time-averaged flow fields of the vortices are measured. In our quasi-one-dimensional setup, there are three stable distances for the drops, which can be characterized by the Faraday wavelength. The interactions of the vortex-mediated bouncing drops are deduced from the streamlines in the liquid bulk. We further show that a three-dimensional vortex ring is induced by a bouncing drop in a square cell.
Dotwave @ 240 frame per Seconds with modified GoPro
This is how precise my temporal resolution can be with my modified goPro and (at last) a good lens : 240 fps ( @848×480 )
Forcing freq is 60 Hz, so Faraday Freq is 30Hz, so for the usual walking mode we have 8 frame during the period of the vertical dynamic. Hence we can observe the dynamic without any strobe effect.
Question: What is the (m, n) mode of the first droplet shown in the movie ?
Uneven Faraday Instability
Faraday instability in a a square container not very well tuned : it has 4 quadrants :
– upper left : a crystal-like pattern
– upper right and lower left : linear pattern
– lower left : below faraday thresold (with a droplet)
Dotwave Sonification
Even if the ear cannot detect any transition on this one, it might give somebody … ideas ?
( Sound is the derivative of the sum of all field values at the center )