Square cavity
Emergent quantization in a square box
Goal of the experiment :
A walking droplet is placed in a square box, at the onset of Faraday thresold.
The trajectory of the droplet is mapped.
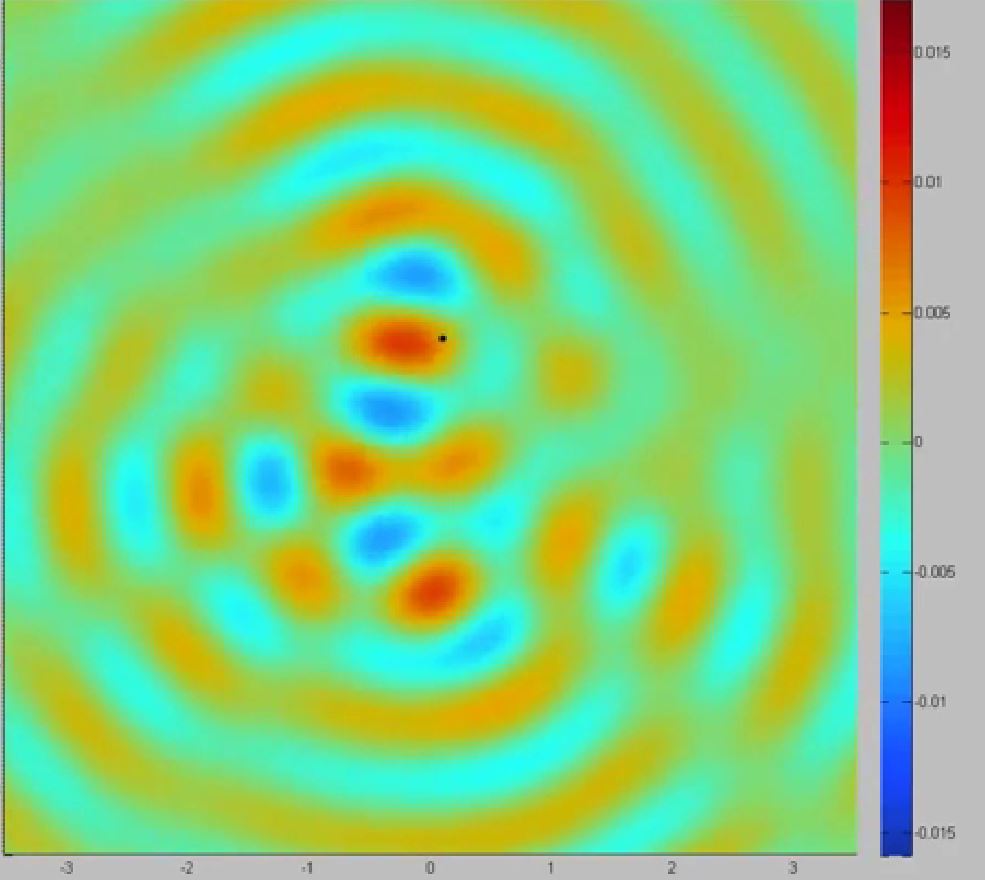
In the long time limit, does a self-interference pattern appear ? what’s its shape ? How does it relate to the square cavity surface wave eigen-modes ?
cf. experiment by Bush et al. : in a circular corral
http://dotwave.org/wavelike-statistics-from-pilot-wave-dynamics-in-a-circular-corral/
In short, we try to reproduce the experiment of Bush et al, but in a square box.
First result :
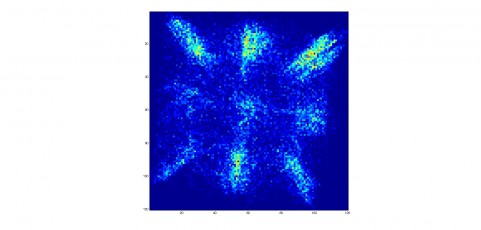
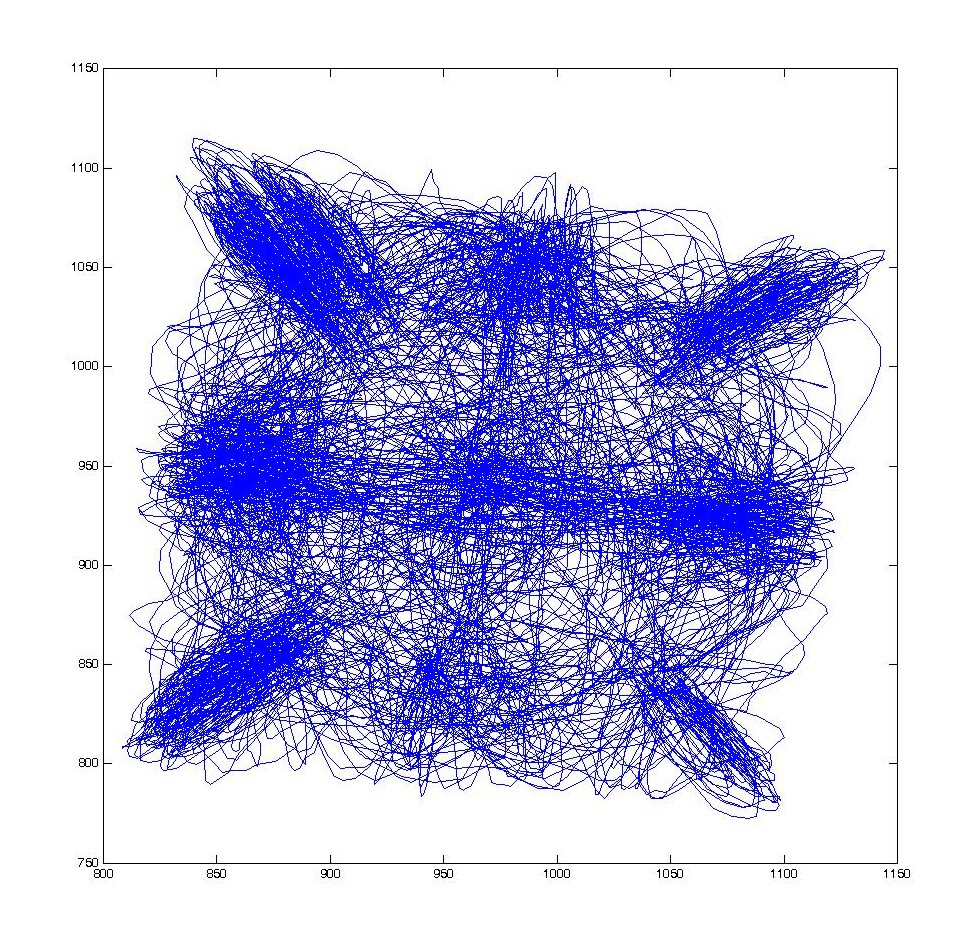
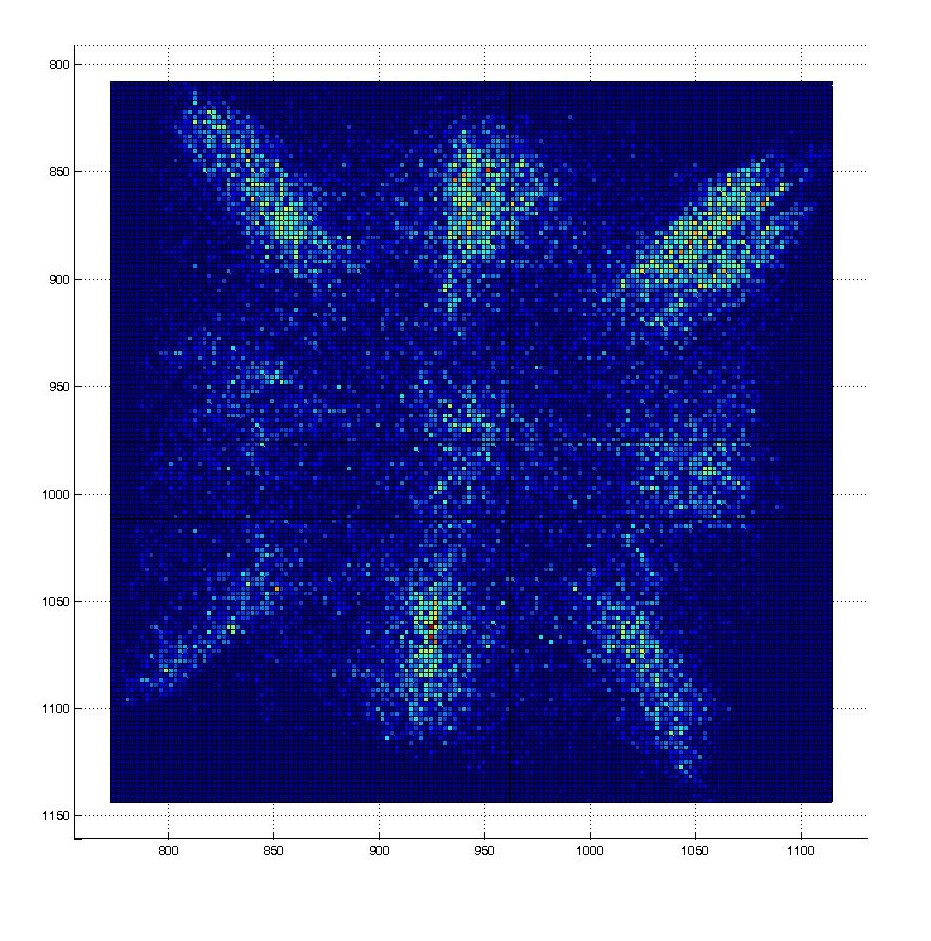
A walking droplet in a square cavity shows random motion, but with time, its trajectory is building a statistic reminiscent of the resonant mode of the cavity.
This can be seen by the naked eye in this movie excerpt :
This is then confirmed with optical tracking measurment of the trajectory :
Trajectory of the walking droplet
The position distribution (~probability density) is then computed :
Probabilty density
PDF Version of this résumé :
Emergent quantization of trajectories in a square box
Birth of a dotwave (Un rebond peut en cacher un autre)
forcing@60Hz
cam@240Hz
Surfer DotWave attached to a spring moving with no viscosity
Surfer attached to a spring moving with no viscosity
Integration of motion equation is done continuously via matlab DELAY DIFERENTIAL EQUATION (ddesd) solver
Hence, the dot “reads” continuously the value of the field
In the mean time, the dot “writes” to the field evry T_F (that is a “bounce”) : at each bounce, a local wave field represented by a Bessel JO function is created, which is then slowly damped (That is the memory Me parameter)
Interferences between the waves created by the last previous 300 bounces (THAT IS THE CUTOFF parameter) are computed at each integration step to obtain the shape of the wave and the motion of the dot.
particle-Wave in a ring : a Dotwave Collisionner
Could such a setup be used to create a microfluidic “in-a-droplet” chemical reactor mixer ?
Classical analog of quantum eigenstate – Orbits and trajectory level
On this video, you’ll see :
– How 2 dotwaves can synchronize on 2 orbits
– How a dotwave can change his orbit (with a little help from the experimentator)
Video shot with a 30 Hz camera, at a forcing frequency of 60 Hz, hence not much stroboscopic flickering
The bath is excited just at the Faraday llevel, or slighly upper.
Dotwave in a box : emergence of normal mode
On this video, the walking droplet is confined in a small cavity (Approx. 6 to 8 times the faraday wavelength)
We observe the emergence of several normal modes of vibration of a walking droplet in a circular corral.
At first, the movement seems “random”, then, the whole wave-particle system synchronizes, and starts turning alltogether.
Differrent modes are possible, with different radius for the droplet trajectory : on this video we see a mode with the droplet on a large radius trajectory, and also a mode where the droplet is on a short radius trajectory
Its seems that thoses radius coincide with with the knots ofs thefaraday standing waves of the cavity, hence we have a quantization of the radius of the different trajectories.