Dynamics and statistics of wave-particle interactions in a confined geometry
Posted by heligone on Apr 10, 2016 in Bibliography, Core Bibliography, Numerical Simulation | 0 comments
Gilet, T. (2014). Dynamics and statistics of wave-particle interactions in a confined geometry. Physical Review E, 90(5), 052917.
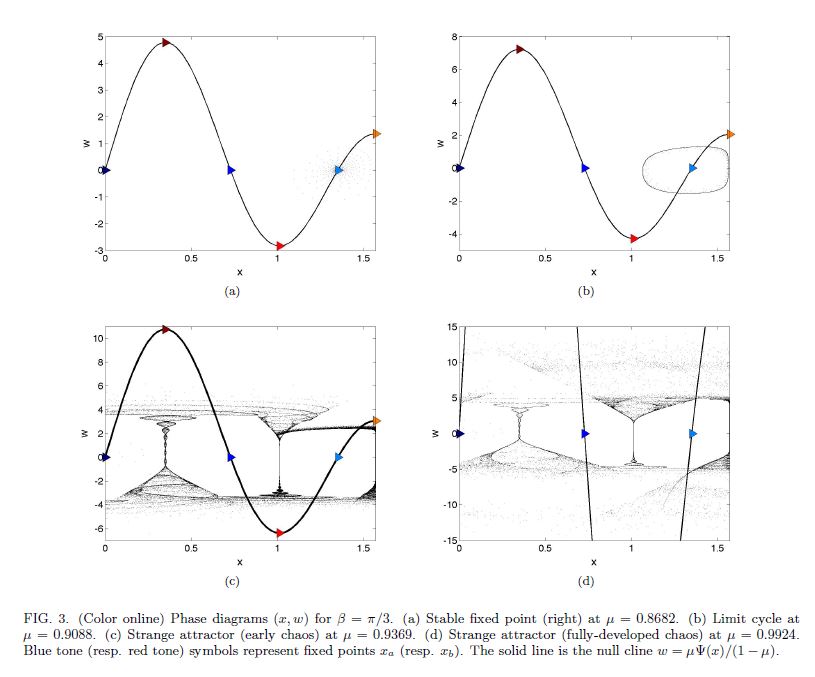
A walker is a droplet bouncing on a liquid surface and propelled by the waves that it generates. This macroscopic wave-particle association exhibits behaviors reminiscent of quantum particles. This article presents a toy model of the coupling between a particle and a confined standing wave. The resulting 2D iterated map captures many features of the walker dynamics observed in different configurations of confinement. These features include the time decomposition of the chaotic trajectory in quantized eigenstates, and the particle statistics being shaped by the wave. It shows that deterministic wave-particle coupling expressed in its simplest form can account for some quantumlike behaviors.
https://orbi.ulg.ac.be/bitstream/2268/178755/2/Generic.pdf
Recent Comments
- Camille on Gravitation
- sam on A low‑cost, precise piezoelectric droplet‑on‑demand generator
- jitendra on A low‑cost, precise piezoelectric droplet‑on‑demand generator
- jitendra on A low‑cost, precise piezoelectric droplet‑on‑demand generator
- yeptube on Statistical projection effects in a hydrodynamic pilot-wave system
- sam on “Tunnel effect “
- Carlos on “Tunnel effect “
- yonglip on Particle in a box – DotWave Self-Interference tracking and statistics
- guest on bouncing droplets
- sam on EmQm17
Categories
- Bibliography (88)
- Blog (43)
- Core Bibliography (75)
- Extended Bibliography (11)
- Featured (14)
- Numerical Simulation (18)
- On the web (4)
- Original Photos (6)
- Original videos (25)
- Photos (14)
- Slider (7)
- Theory Bibliography (18)
- Thesis (7)
- Videos (33)
Other Research teams
- Austrian Institute for Nonlinear Studies (AINS) – Gerhard Groessing
- Berkeley University – TAF LAB
- Caltech Mc Keon Research Group
- Instituto Nacional de Matemática Pura e Aplicada – Andre Nachbin and Carlos Galeano
- MIT – John BUSH
- St. Petersburg Nuclear Physics Institute – Dr. Valeriy Sbitnev
- Università degli Studi di Palermo – Pr. Diego Molteni –
- Université de Liège – Quandrops
- Université Paris Diderot – Yves Couder
- University of Bath – PAUL MILEWSKI
- University of Cambridge – Computer Laboratory – Dr Robert Brady
Liens
Recent Posts
- Spontaneous emergence of a spin state for an emitter in a time-varying medium June 9, 2022
- Spin Lattice of walking droplets June 20, 2018
- Statistical projection effects in a hydrodynamic pilot-wave system June 19, 2018
- Quantum physics Dropwise June 18, 2018
- EmQm17 October 22, 2017
- Walking droplet above cavities October 17, 2017
- Faraday wave droplet dynamics : discret time analysis October 17, 2017
- Tunneling with a hydrodynamic pilot-wave model October 17, 2017
- Walking droplets in linear channels October 17, 2017
- Self-propulsion and crossing statistics under random initial conditions October 17, 2017
- A trajectory equation for walking droplets : hydrodynamic pilot-wave theory October 17, 2017
- Influence of memory on trajectory in a harmonic potential January 22, 2017
- A model for Faraday pilot waves over variable topography January 22, 2017
- Non-specular reflection of walking droplets January 22, 2017
- Self-attraction into spinning eigenstates of a mobile wave source by its emission back-reaction January 22, 2017
- Onset of chaos in orbital pilot-wave dynamics January 15, 2017
- Surface topography measurements of the bouncing droplet experiment December 4, 2016
- Momentum exchange in the electron double-slit experiment November 29, 2016
- Double-slit experiment with single wave-driven particles and its relation to quantum mechanics October 12, 2016
- New reference website from Paris Couder & Fort Team October 7, 2016
- Shedding light on pilot-wave phenomena September 17, 2016
- Neimark–Sacker bifurcation and evidence of chaos in a discrete dynamical model of walkers September 17, 2016
- Wave-Based Turing Machine: Time Reversal and Information Erasing September 17, 2016
- Transition Orbits of Walking Droplets August 15, 2016
- emergence of statistical pattern in a 1D cavity August 5, 2016
- Quantumlike statistics of deterministic waveparticle interactions in a circular cavity July 13, 2016
- Retro-influence of a square cavity on a circular standing wave May 22, 2016
- Square cavity May 22, 2016
- Rainbow colored dotwave May 22, 2016
- Dotwave picture on Phys.org May 22, 2016
- Faraday wave lattice as an elastic metamaterial May 22, 2016
- Scattering theory of walking droplets in the presence of obstacles May 22, 2016
- Nonlinear Generation of Vorticity by Surface Waves May 21, 2016
- Pilot-wave dynamics in a harmonic potential : Quantization and stability of circular orbits May 2, 2016
- Physics Today : letters to the editor April 11, 2016
- Faraday pilot wave dynamics : modelling and computation April 10, 2016
- Dynamics and statistics of wave-particle interactions in a confined geometry April 10, 2016
- Displacement of an Electrically Charged Drop on a Vibrating Bath April 10, 2016
- Emergent quantization in a square box April 5, 2016
- Mini Colloque RNL 2016 : Dualité onde-corpuscule à l’échelle macroscopique March 15, 2016
- Smoothed Particles Hydrodynamics numerical simulations of droplets walking on viscous vibrating fluid January 25, 2016
- Revisiting time reversal and holography with spacetime transformations. October 12, 2015
- Waveguides for walking droplets October 12, 2015
- Pilot-Wave Hydrodynamics (Annual Review of Fluid Mechanics 2015) September 26, 2015
- On the analogy of quantum wave-particle duality with bouncing droplets September 26, 2015
- Strings of droplets propelled by coherent waves September 26, 2015
- Interaction of two walkers: Wave-mediated energy and force September 26, 2015
- Build-up of macroscopic eigenstates in a memory-based constrained system September 25, 2015
- Parametrically excited water surface ripples as ensembles of oscillons September 24, 2015
- DotWave Keynote at XLIM Lab in Limoges June 19, 2015
- Une mémoire ondulatoire : États propres, Chaos et Probabilités June 12, 2015
- The wave-induced added mass of walking droplets May 12, 2015
- Generating uniaxial vibration with an electrodynamic shaker and external air bearing May 12, 2015
- A low‑cost, precise piezoelectric droplet‑on‑demand generator May 12, 2015
- Chaos Driven by Interfering Memory May 12, 2015
- Étude d’une dynamique à mémoire de chemin: une expérimentation théorique May 12, 2015
- “Fingers and Holes in a Shaken Cornstrach Solution” sur YouTube August 17, 2014
- Birth of a dotwave (Un rebond peut en cacher un autre) August 3, 2014
- Video Lesson – 07/06/2013 – Hydrodynamic Modelling of Pilot-Wave and boucing droplet coupling in a Faraday Problem July 21, 2014
- Bouncing droplet project — single-slit diffraction July 21, 2014
Recent Comments
- Camille on Gravitation
- sam on A low‑cost, precise piezoelectric droplet‑on‑demand generator
- jitendra on A low‑cost, precise piezoelectric droplet‑on‑demand generator
- jitendra on A low‑cost, precise piezoelectric droplet‑on‑demand generator
- yeptube on Statistical projection effects in a hydrodynamic pilot-wave system
- sam on “Tunnel effect “
- Carlos on “Tunnel effect “
- yonglip on Particle in a box – DotWave Self-Interference tracking and statistics
- guest on bouncing droplets
- sam on EmQm17
Recent Posts
- Spontaneous emergence of a spin state for an emitter in a time-varying medium
- Spin Lattice of walking droplets
- Statistical projection effects in a hydrodynamic pilot-wave system
- Quantum physics Dropwise
- EmQm17
- Walking droplet above cavities
- Faraday wave droplet dynamics : discret time analysis
- Tunneling with a hydrodynamic pilot-wave model
- Walking droplets in linear channels
- Self-propulsion and crossing statistics under random initial conditions
- A trajectory equation for walking droplets : hydrodynamic pilot-wave theory
- Influence of memory on trajectory in a harmonic potential
- A model for Faraday pilot waves over variable topography
- Non-specular reflection of walking droplets
- Self-attraction into spinning eigenstates of a mobile wave source by its emission back-reaction
Random Video
Other Research teams
- Austrian Institute for Nonlinear Studies (AINS) – Gerhard Groessing
- Berkeley University – TAF LAB
- Caltech Mc Keon Research Group
- Instituto Nacional de Matemática Pura e Aplicada – Andre Nachbin and Carlos Galeano
- MIT – John BUSH
- St. Petersburg Nuclear Physics Institute – Dr. Valeriy Sbitnev
- Università degli Studi di Palermo – Pr. Diego Molteni –
- Université de Liège – Quandrops
- Université Paris Diderot – Yves Couder
- University of Bath – PAUL MILEWSKI
- University of Cambridge – Computer Laboratory – Dr Robert Brady
Like !
Authors
About
Dotwave.org is an Independant research group
You can check more
- Discussions on current research on this Facebook public page :
- videos on these youtube channels :
All photos and videos presented on this website are our own work unless mentionned otherwise, or included in the "bibliography" section.