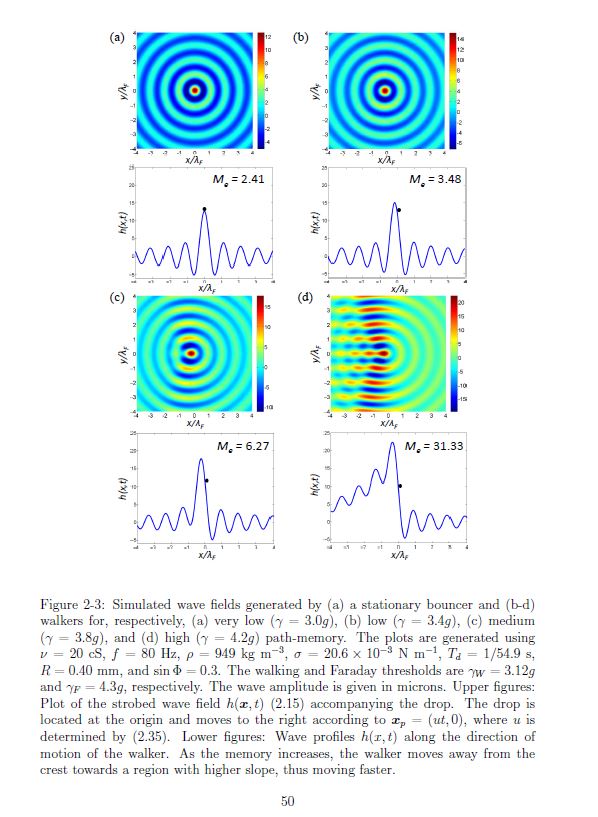
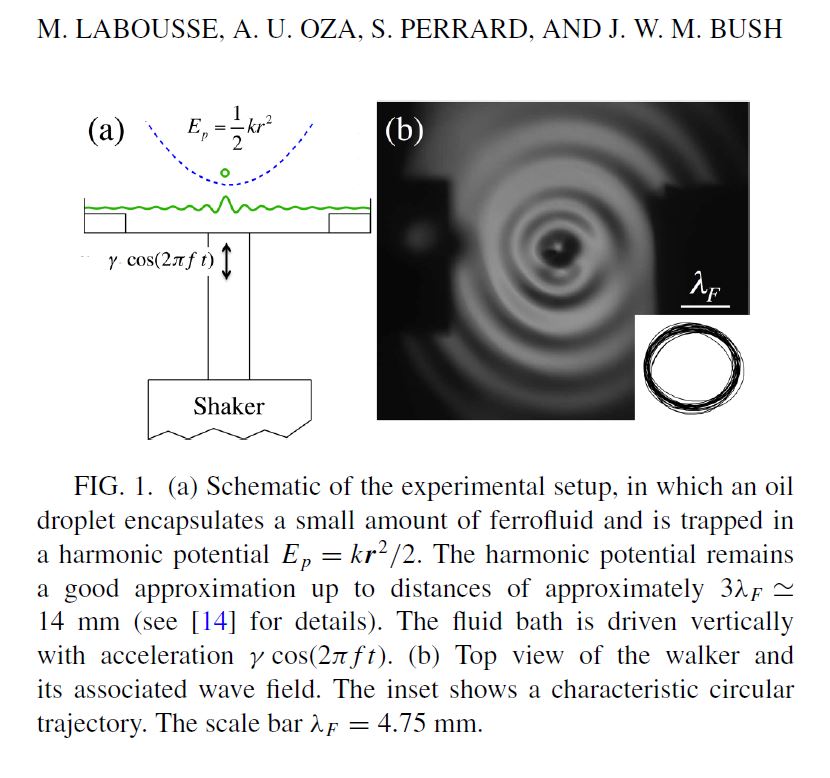
ABSTRACT  : “Yves Couder and coworkers have demonstrated that millimetric droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic quantum realm, including single-particle diffraction, tunneling, quantized orbits, and wave-like statistics in a corral. We here develop an integro-differential trajectory equation for these walking droplets with a view to gaining insight into their subtle dynamics. The orbital quantization is rationalized by assessing the stability of the orbital solutions. The stability analysis also predicts the existence of wobbling orbital states reported in recent experiments, and the absence of stable orbits in the limit of large vibrational forcing. In this limit, the complex walker dynamics give rise to a coherent statistical behavior with wave-like features. We characterize the progression from quantized orbits to chaotic dynamics as the vibrational forcing is increased progressively. We then describe the dynamics of a weakly-accelerating walker in terms of its wave-induced added mass, which provides rationale for the anomalously large orbital radii observed in experiments.”

Oza, A. U. (2014). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory (Doctoral dissertation, Massachusetts Institute of Technology).

https://dspace.mit.edu/bitstream/handle/1721.1/90191/890211673-MIT.pdf?sequence=2

Abstract  : We examine the orbital dynamics of droplets self-propelling along the surface of a vibrating bath. Circular orbital motion may arise when the walking droplet is subjected to one of three external force fields, the Coriolis force, a simple harmonic force, and a Coulomb force. Particular attention is given to a theoretical characterization of the onset of chaos that accompanies the destabilization of such circular orbits.

Tambasco, L., Harris, D., Oza, A., Rosales, R., & Bush, J. (2015, November). Onset of chaos in orbital pilot-wave dynamics. In APS Meeting Abstracts.

Paper available on researchgate.net/ (Requires free login)

Labousse, M., Oza, A. U., Perrard, S., & Bush, J. W. (2016). Pilot-wave dynamics in a harmonic potential: Quantization and stability of circular orbits.Physical Review E, 93(3), 033122.

“We present the results of a theoretical investigation of the dynamics of a droplet walking on a vibrating fluid bath under the influence of a harmonic potential. The walking droplet’s horizontal motion is described by an integro-differential trajectory equation, which is found to admit steady orbital solutions. Predictions for the dependence of the orbital radius and frequency on the strength of the radial harmonic force field agree favorably with experimental data. The orbital quantization is rationalized through an analysis of the orbital solutions. The predicted dependence of the orbital stability on system parameters is compared with experimental data and the limitations of the model are discussed.”

http://arxiv.org/pdf/1604.07394

Bush, J. W., Oza, A. U., & Moláček, J. (2014). The wave-induced added mass of walking droplets. Journal of Fluid Mechanics, 755, R7.

It has recently been demonstrated that droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic realm. The walker, consisting of a droplet plus its guiding wavefield, is a spatially extended object. We here examine the dependence of the walker mass and momentum on its velocity. Doing so indicates that, when the walker’s time scale of acceleration is long relative to the wave decay time, its dynamics may be described in terms of the mechanics of a particle with a speed-dependent mass and a nonlinear drag force that drives it towards a fixed speed. Drawing an analogy with relativistic mechanics, we define a hydrodynamic boost factor for the walkers. This perspective provides a new rationale for the anomalous orbital radii reported in recent studies

Click to access Boost-JFM.pdf

Oza, A. U., Harris, D. M., Rosales, R. R., & Bush, J. W. (2014). Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization. Journal of Fluid Mechanics, 744, 404-429.

We present the results of a theoretical investigation of droplets walking on a
rotating vibrating fluid bath. The droplet’s trajectory is described in terms of an
integro-differential equation that incorporates the influence of its propulsive wave
force. Predictions for the dependence of the orbital radius on the bath’s rotation
rate compare favourably with experimental data and capture the progression from
continuous to quantized orbits as the vibrational acceleration is increased. The orbital
quantization is rationalized by assessing the stability of the orbital solutions, and may
be understood as resulting directly from the dynamic constraint imposed on the drop
by its monochromatic guiding wave. The stability analysis also predicts the existence
of wobbling orbital states reported in recent experiments, and the absence of stable
orbits in the limit of large vibrational forcing

http://math.mit.edu/~auoza/JFM_2.pdf

Oza, A. U., Rosales, R. R., & Bush, J. W. (2013). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. Journal of Fluid Mechanics,737, 552-570.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/12/ORB-JFM.pdf

Integro-differential equation describing the horizontal motion of a walking droplet

Stability to perturbations