Chu, H. Y., & Fei, H. T. (2014). Vortex-mediated bouncing drops on an oscillating liquid. Physical Review E, 89(6), 063011

 http://journals.aps.org/pre/abstract/10.1103/PhysRevE.89.063011 (Subsrciption required)

Stunning Vizualisization of undersurface flows

Abstract :

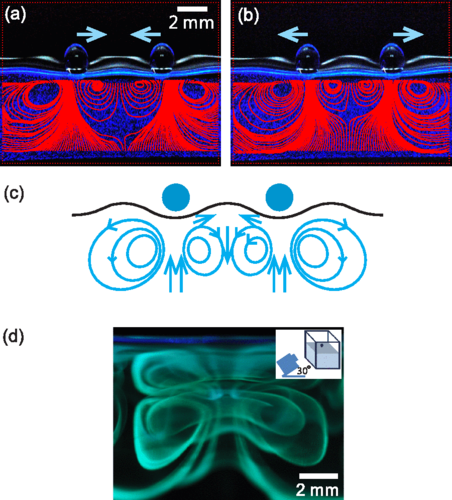
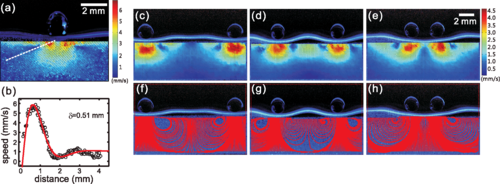
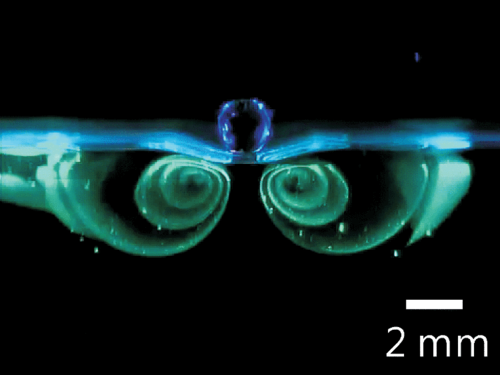
We have investigated the behavior of bouncing drops on a liquid surface by using particle image velocimetry analysis. A drop on an oscillating liquid surface is observed to not coalesce with the liquid and to travel along the surface if the oscillation is strong enough. A streaming vortex pair, induced by the alternatively distorted liquid surface, shows up below a bouncing drop. The time-averaged flow fields of the vortices are measured. In our quasi-one-dimensional setup, there are three stable distances for the drops, which can be characterized by the Faraday wavelength. The interactions of the vortex-mediated bouncing drops are deduced from the streamlines in the liquid bulk. We further show that a three-dimensional vortex ring is induced by a bouncing drop in a square cell.

Andersen, A., Madsen, J., Reichelt, C., Ahl, S. R., Lautrup, B., Ellegaard, C., … & Bohr, T. (2014). Comment on Y. Couder and E. Fort:” Single-Particle Diffraction and Interference at a Macroscopic Scale”, Phys. Rev. Lett.(2006).arXiv preprint arXiv:1405.0466.

Where a danish team argue that Couder’sDouble Slit Experiment reported in  Single-Particle Diffraction and Interference at a Macroscopic Scale   is not convincing.

They tried to replicate the experiment but they did not manage.

Plus : a quick report of a numerical experimentation of Schrödinger equation with a “”walker-like”  source term

Abstract :

In a paper from 2006, Couder and Fort [1] describe a version of the famous double slit experiment performed with drops bouncing on a vibrated fluid surface, where interference in the particle statistics is found even though it is possible to determine unambiguously which slit the “walking” drop passes. It is one of the first papers in an impressive series, showing that such walking drops closely resemble de Broglie waves and can reproduce typical quantum phenomena like tunneling and quantized states [2–13]. The double slit experiment is, however, a more stringent test of quantum mechanics, because it relies upon superposition and phase coherence. In the present comment we first point out that the experimental data presented in [1] are not convincing, and secondly we argue that it is not possible in general to capture quantum mechanical results in a system, where the trajectory of the particle is well-defined.

http://arxiv.org/pdf/1405.0466.pdf

Keywords : Madelung-Bohm equation

Oza, A. U., Harris, D. M., Rosales, R. R., & Bush, J. W. (2014). Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization. Journal of Fluid Mechanics, 744, 404-429.

We present the results of a theoretical investigation of droplets walking on a
rotating vibrating fluid bath. The droplet’s trajectory is described in terms of an
integro-differential equation that incorporates the influence of its propulsive wave
force. Predictions for the dependence of the orbital radius on the bath’s rotation
rate compare favourably with experimental data and capture the progression from
continuous to quantized orbits as the vibrational acceleration is increased. The orbital
quantization is rationalized by assessing the stability of the orbital solutions, and may
be understood as resulting directly from the dynamic constraint imposed on the drop
by its monochromatic guiding wave. The stability analysis also predicts the existence
of wobbling orbital states reported in recent experiments, and the absence of stable
orbits in the limit of large vibrational forcing

http://math.mit.edu/~auoza/JFM_2.pdf

Perrard, S., Labousse, M., Miskin, M., Fort, E., & Couder, Y. (2014). Self-organization into quantized eigenstates of a classical wave-driven particle.Nature communications, 5.

A growing number of dynamical situations involve the coupling of particles or singularities with physical waves. In principle these situations are very far from the wave particle duality at quantum scale where the wave is probabilistic by nature. Yet some dual characteristics were observed in a system where a macroscopic droplet is guided by a pilot wave it generates. Here we investigate the behaviour of these entities when confined in a two-dimensional harmonic potential well. A discrete set of stable orbits is observed, in the shape of successive generalized Cassinian-like curves (circles, ovals, lemniscates, trefoils and so on). Along these specific trajectories, the droplet motion is characterized by a double quantization of the orbit spatial extent and of the angular momentum. We show that these trajectories are intertwined with the dynamical build-up of central wave-field modes. These dual self-organized modes form a basis of eigenstates on which more complex motions are naturally decomposed.

http://www.nature.com/ncomms/2014/140130/ncomms4219/full/ncomms4219.html

http://arxiv.org/ftp/arxiv/papers/1402/1402.1423.pdf

Quantization of trajectories of a dotwave in a harmonic potential

Shirokoff, D. (2013). Bouncing droplets on a billiard table. Chaos: An Interdisciplinary Journal of Nonlinear Science, 23(1), 013115.

http://arxiv.org/pdf/1203.2204.pdf

Discrete numerical simulation

Attractor ets

Perrard, S., Labousse, M., Miskin, M., Fort, E., & Couder, Y. Effets de quantification d’une association onde-particule soumise à une force centrale.Résumés des exposés de la 16e Rencontre du Non-Linéaire Paris 2013, 68.

http://nonlineaire.univ-lille1.fr/SNL/media/2012/CR/Perrard.pdf

eigenstates in circular cavity

Harris, D. M., & Bush, J. W. (2014). Droplets walking in a rotating frame: from quantized orbits to multimodal statistics. Journal of Fluid Mechanics, 739, 444-464.

We present the results of an experimental investigation of a droplet walking on the
surface of a vibrating rotating fluid bath. Particular attention is given to demonstrating
that the stable quantized orbits reported by Fort et al. (Proc. Natl Acad. Sci.,
vol. 107, 2010, pp. 17515–17520) arise only for a finite range of vibrational
forcing, above which complex trajectories with multimodal statistics arise. We first
present a detailed characterization of the emergence of orbital quantization, and
then examine the system behaviour at higher driving amplitudes. As the vibrational
forcing is increased progressively, stable circular orbits are succeeded by wobbling
orbits with, in turn, stationary and drifting orbital centres. Subsequently, there is a
transition to wobble-and-leap dynamics, in which wobbling of increasing amplitude
about a stationary centre is punctuated by the orbital centre leaping approximately
half a Faraday wavelength. Finally, in the limit of high vibrational forcing, irregular
trajectories emerge, characterized by a multimodal probability distribution that reflects
the persistent dynamic influence of the unstable orbital states.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2014/01/HB-JFM-2014.pdf

Robert Brady, Ross Anderson. Jan 16, 2014.

http://arxiv.org/pdf/1401.4356v1.pdf

review of all analogies between dotwaves mechanics and quantum mechanics.

Sbitnev, V. I. (2013). Droplets moving on a fluid surface: interference pattern from two slits. arXiv preprint arXiv:1307.6920.

http://arxiv.org/pdf/1307.6920.pdf

Feynman path integral approach

Droplet / Antidroplet

Soliton diffraction

Oza, A. U., Rosales, R. R., & Bush, J. W. (2013). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. Journal of Fluid Mechanics,737, 552-570.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/12/ORB-JFM.pdf

Integro-differential equation describing the horizontal motion of a walking droplet

Stability to perturbations

Moláček, J., & Bush, J. W. (2013). Drops bouncing on a vibrating bath. Journal of Fluid Mechanics, 727, 582-611.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB1-2013.pdf

Linear and logarithmic  spring model of a boucing droplet

Wind-Willassen, Ø., Moláček, J., Harris, D. M., & Bush, J. W. (2013). Exotic states of bouncing and walking droplets. Physics of Fluids, 25, 082002.

http://windw.dk/2013Bouncing.pdf

Phase diagram refinement : the different styles of bouncing

Moláček, J., & Bush, J. W. (2013). Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory. Journal of Fluid Mechanics, 727, 582-617.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB2-2013.pdf

The most advanced theoretical model

Harris, D. M., Moukhtar, J., Fort, E., Couder, Y., & Bush, J. W. (2013). Wavelike statistics from pilot-wave dynamics in a circular corral. Physical Review E, 88(1), 011001.

Abstract : Bouncing droplets can self-propel laterally along the surface of a vibrated fluid bath by virtue of a resonant interaction with their own wave field. The resulting walking droplets exhibit features reminiscent of microscopic quantum particles. Here we present the results of an experimental investigation of droplets walking in a circular corral. We demonstrate that a coherent wavelike statistical behavior emerges from the complex underlying dynamics and that the probability distribution is prescribed by the Faraday wave mode of the corral. The statistical behavior of the walking droplets is demonstrated to be analogous to that of electrons in quantum corrals.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/Harris-Corrals-2013.pdf

Statistical behavior of a walking droplet in a confined geometry

Eddi, A., Decelle, A., Fort, E., & Couder, Y. (2009). Archimedean lattices in the bound states of wave interacting particles. EPL (Europhysics Letters), 87(5), 56002.

http://stilton.tnw.utwente.nl/people/eddi/Papers/epl_Cristaux.pdf

Cristal lattices of bouncing droplets

Fort, E., Eddi, A., Boudaoud, A., Moukhtar, J., & Couder, Y. (2010). Path-memory induced quantization of classical orbits. Proceedings of the National Academy of Sciences, 107(41), 17515-17520.

http://stilton.tnw.utwente.nl/people/eddi/Papers/PNAS_2010.pdf

Rotating bath

Quantization of trajectories

“L’organisation du manuscrit est la suivante : dans le premier chapitre, nous rappelons les premieres experiences realisees avec les gouttes rebondissantes, en particulier les regimes ou elles sont statiques. Nous presentons egalement l’instabilite de Faraday qui permet d’expliquer le couplage entre goutte et ondes a l’origine des marcheurs. Leurs proprietes sont discutees, en particulier dans le cas des experiences de diraction. Dans un second chapitre, nous presentons le montage experimental ainsi que l’ensemble des techniques de mesure utilisees. Le troisieme chapitre est dedie a l’etude d’un analogue de l’eet tunnel pour les marcheurs. Le quatrieme est consacre a l’etude des ondes de surface generees par un marcheur, en particulier le lien avec l’instabilite de Faraday a l’origine de la memoire de chemin. Enfin, dans le chapitre cinq, nous analysons la nature des trajectoires circulaires d’un marcheur soumis a une force orthogonale au mouvement. L’in uence de la memoire de chemin sur la quantication des rayons est presentee en detail, pour comprendre comment cet analogue macroscopique des niveaux de Landau se met en place avec des marcheurs.”

Eddi, A. (2011). Marcheurs, Dualité onde-particule et Mémoire de chemin (Doctoral dissertation, Université Paris-Diderot-Paris VII).

http://tel.archives-ouvertes.fr/docs/00/57/56/26/PDF/these_A_Eddi.pdf

Terwagne, D., Ludewig, F., Vandewalle, N., & Dorbolo, S. (2013). The role of the droplet deformations in the bouncing droplet dynamics. Physics of Fluids (1994-present), 25(12), 122101.

http://www.grasp.ulg.ac.be/article/2013_terwagne_POF.pdf

ArXiv Preprint  :

Terwagne, D., Ludewig, F., Vandewalle, N., & Dorbolo, S. (2013). The role of deformations in the bouncing droplet dynamics. arXiv preprint arXiv:1301.7463.

http://arxiv.org/pdf/1301.7463v1.pdf

Editor Postprint :

http://orbi.ulg.ac.be/handle/2268/159838

Automatic droplet generator

Period doubling transition of bouncing droplet, bifurcation diagram

Simulation with mass-spring system

Terwagne, D. (2011). Bouncing droplets, the role of deformations.

http://bictel.ulg.ac.be/ETD-db/collection/available/ULgetd-09262011-010800/unrestricted/2011_Terwagne_these.pdf

APENDIX C describes a automatic droplet generator

A GREAT video by John BUSH and his team at MIT