particle-Wave in a ring : a Dotwave Collisionner
Read MoreEffets de quantification d’une association onde-particule soumise à une force centrale
Perrard, S., Labousse, M., Miskin, M., Fort, E., & Couder, Y. Effets de quantification d’une association onde-particule soumise à une force centrale.Résumés des exposés de la 16e Rencontre du Non-Linéaire Paris 2013, 68.
http://nonlineaire.univ-lille1.fr/SNL/media/2012/CR/Perrard.pdf
eigenstates in circular cavity
The Feynman Lectures on Physics : Quantum behavior
Where it all started …
Controlled double-slit electron diffraction : reproduction of the famous Feynman 1965 thought experiment.
Bach, R., Pope, D., Liou, S. H., & Batelaan, H. (2013). Controlled double-slit electron diffraction. New Journal of Physics, 15(3), 033018.
http://iopscience.iop.org/1367-2630/15/3/033018/pdf/1367-2630_15_3_033018.pdf
And some movies of the interference pattern build-up :
http://iopscience.iop.org/1367-2630/15/3/033018/media
The famous Feynman thought experiment reproduced ! ((cf. Feynman Lectures on Physics, vol III, figures 1–3,))
Confinement of electrons to quantum corrals on a metal surface
Crommie, M. F., Lutz, C. P., & Eigler, D. M. (1993). Confinement of electrons to quantum corrals on a metal surface. Science, 262(5131), 218-220.
http://users.phys.psu.edu/~rick/MATH/LECTURES/LECT13/PDF/eigler_circular_corral.pdf
Droplets walking in a rotating frame: from quantized orbits to multimodal statistics
Harris, D. M., & Bush, J. W. (2014). Droplets walking in a rotating frame: from quantized orbits to multimodal statistics. Journal of Fluid Mechanics, 739, 444-464.
We present the results of an experimental investigation of a droplet walking on the
surface of a vibrating rotating fluid bath. Particular attention is given to demonstrating
that the stable quantized orbits reported by Fort et al. (Proc. Natl Acad. Sci.,
vol. 107, 2010, pp. 17515–17520) arise only for a finite range of vibrational
forcing, above which complex trajectories with multimodal statistics arise. We first
present a detailed characterization of the emergence of orbital quantization, and
then examine the system behaviour at higher driving amplitudes. As the vibrational
forcing is increased progressively, stable circular orbits are succeeded by wobbling
orbits with, in turn, stationary and drifting orbital centres. Subsequently, there is a
transition to wobble-and-leap dynamics, in which wobbling of increasing amplitude
about a stationary centre is punctuated by the orbital centre leaping approximately
half a Faraday wavelength. Finally, in the limit of high vibrational forcing, irregular
trajectories emerge, characterized by a multimodal probability distribution that reflects
the persistent dynamic influence of the unstable orbital states.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2014/01/HB-JFM-2014.pdf
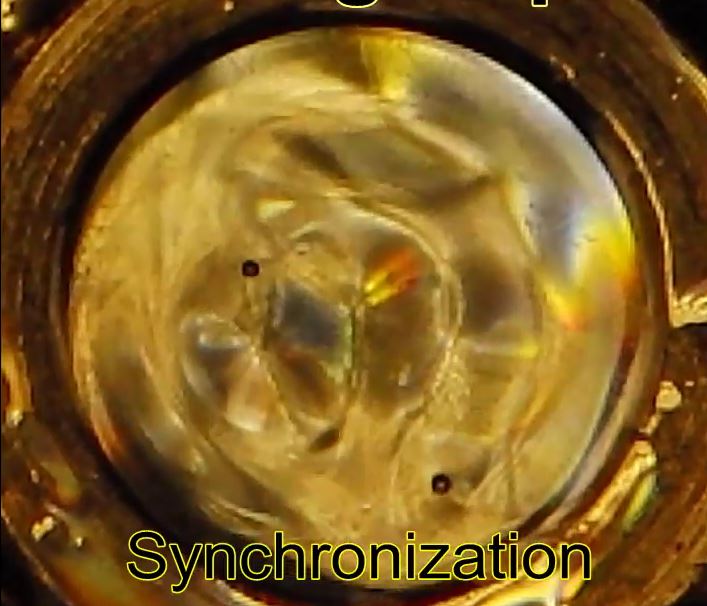
Classical analog of quantum eigenstate – Orbits and trajectory level
On this video, you’ll see :
– How 2 dotwaves can synchronize on 2 orbits
– How a dotwave can change his orbit (with a little help from the experimentator)
Video shot with a 30 Hz camera, at a forcing frequency of 60 Hz, hence not much stroboscopic flickering
The bath is excited just at the Faraday llevel, or slighly upper.
Why bouncing droplets are a pretty good model of quantum mechanics
Robert Brady, Ross Anderson. Jan 16, 2014.
http://arxiv.org/pdf/1401.4356v1.pdf
review of all analogies between dotwaves mechanics and quantum mechanics.
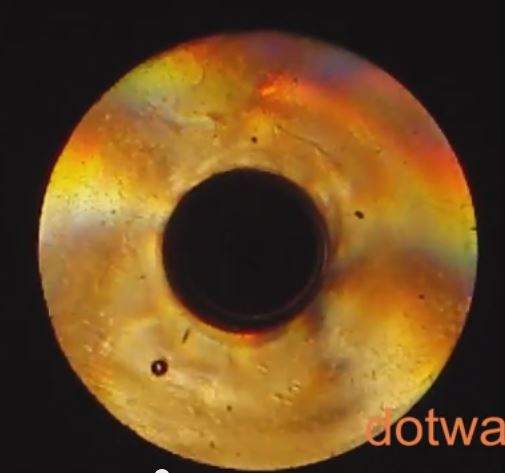
Dotwave in a box : emergence of normal mode
On this video, the walking droplet is confined in a small cavity (Approx. 6 to 8 times the faraday wavelength)
We observe the emergence of several normal modes of vibration of a walking droplet in a circular corral.
At first, the movement seems “random”, then, the whole wave-particle system synchronizes, and starts turning alltogether.
Differrent modes are possible, with different radius for the droplet trajectory : on this video we see a mode with the droplet on a large radius trajectory, and also a mode where the droplet is on a short radius trajectory
Its seems that thoses radius coincide with with the knots ofs thefaraday standing waves of the cavity, hence we have a quantization of the radius of the different trajectories.
How it is done : DIY Cymatronics
A Transparent plate is mounted (via magnets) to three loud peakers serial-connected to an amplifier delivering a sinus signal.
Silicon oil ( with viscosuity 20 Cst) is put on the transparent plate.
A point source light is collimated, goes through the oil
A mirror placed below redirects the light beam to tha camera.
NB : it is not easy to set up this light system : the light source muste precisely tuned at the focal point of the lens.
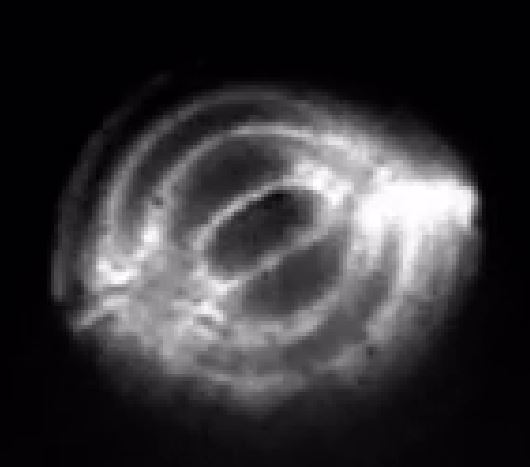
Vibration modes of a walking droplet trapped in a small circular box
When a walking droplet is trapped in a small box, the waves that it has generated extends to the whole frame.
Thus those waves can resonate and form normal modes of vibration inside the cavity.
The droplet is then forced to move according to this normal wave field
DotWave at sunset
Read MoreWave mediated interaction
Read MoreDroplets moving on a fluid surface: interference pattern from two slits
Sbitnev, V. I. (2013). Droplets moving on a fluid surface: interference pattern from two slits. arXiv preprint arXiv:1307.6920.
http://arxiv.org/pdf/1307.6920.pdf
Feynman path integral approach
Droplet / Antidroplet
Soliton diffraction
A suggested interpretation of the quantum theory in terms of” hidden” variables. I
Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of” hidden” variables. I. Physical Review, 85(2), 166.
http://www.psiquadrat.de/downloads/bohm52a.pdf
Hidden variable theory foundation
A trajectory equation for walking droplets: hydrodynamic pilot-wave theory
Oza, A. U., Rosales, R. R., & Bush, J. W. (2013). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. Journal of Fluid Mechanics,737, 552-570.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/12/ORB-JFM.pdf
Integro-differential equation describing the horizontal motion of a walking droplet
Stability to perturbations
Drops bouncing on a vibrating bath
Moláček, J., & Bush, J. W. (2013). Drops bouncing on a vibrating bath. Journal of Fluid Mechanics, 727, 582-611.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB1-2013.pdf
Linear and logarithmic spring model of a boucing droplet
Exotic states of bouncing and walking droplets
Wind-Willassen, Ø., Moláček, J., Harris, D. M., & Bush, J. W. (2013). Exotic states of bouncing and walking droplets. Physics of Fluids, 25, 082002.
http://windw.dk/2013Bouncing.pdf
Phase diagram refinement : the different styles of bouncing
Drops walking on a vibrating bath : towards a hydrodynamic wave theory
Moláček, J., & Bush, J. W. (2013). Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory. Journal of Fluid Mechanics, 727, 582-617.
http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB2-2013.pdf
The most advanced theoretical model