Square cavity
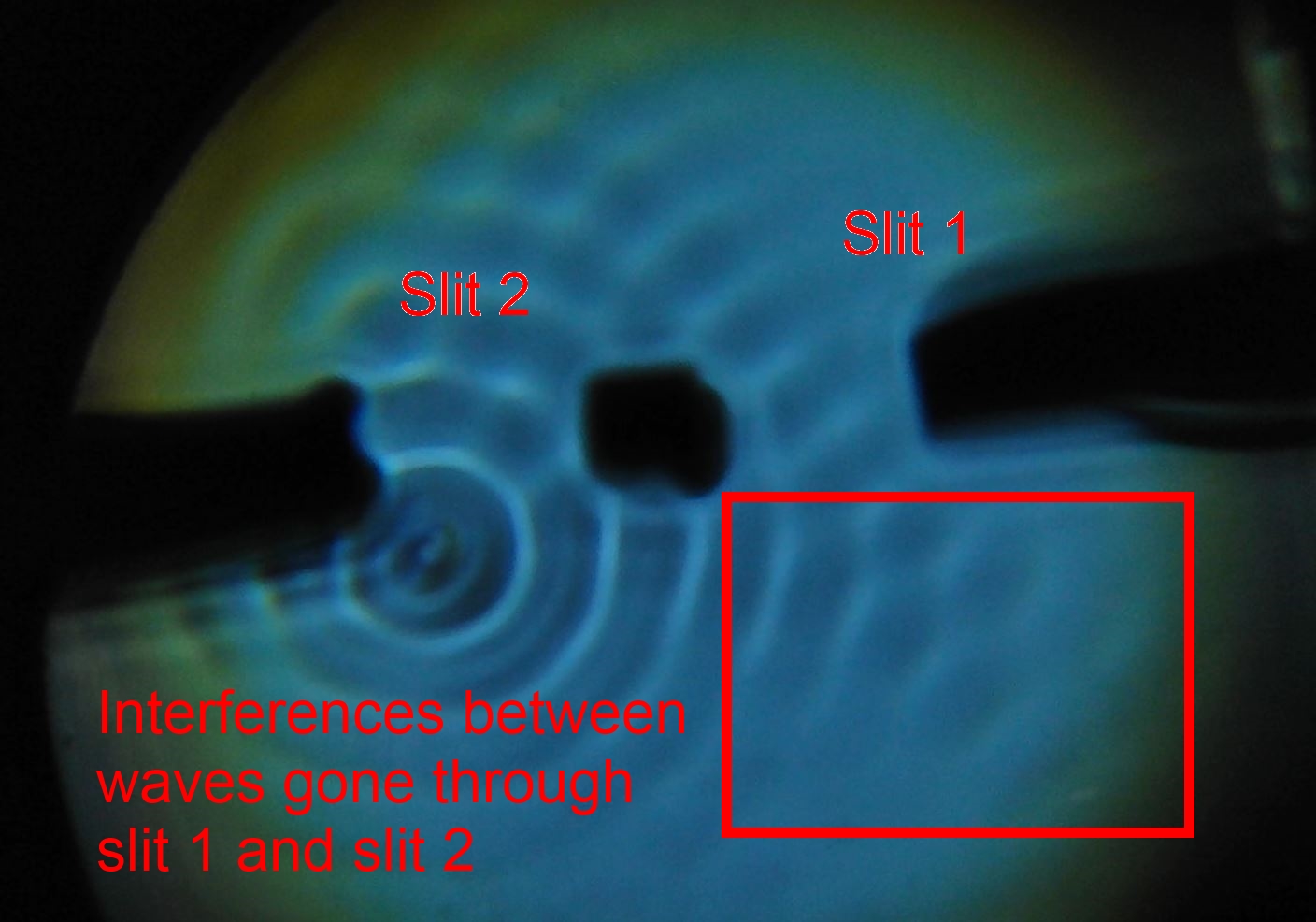
Birth of a dotwave (Un rebond peut en cacher un autre)
forcing@60Hz
cam@240Hz
Dotwave @ 240 frame per Seconds with modified GoPro
This is how precise my temporal resolution can be with my modified goPro and (at last) a good lens : 240 fps ( @848×480 )
Forcing freq is 60 Hz, so Faraday Freq is 30Hz, so for the usual walking mode we have 8 frame during the period of the vertical dynamic. Hence we can observe the dynamic without any strobe effect.
Question: What is the (m, n) mode of the first droplet shown in the movie ?
Dotwave Sonification
Even if the ear cannot detect any transition on this one, it might give somebody … ideas ?
( Sound is the derivative of the sum of all field values at the center )
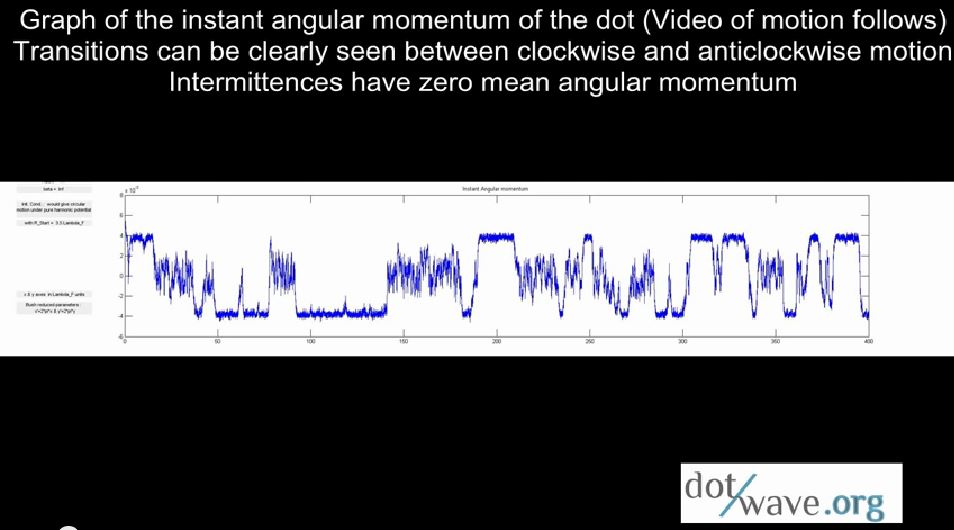
Spin Inversion : deterministic & chaotic superposition
On this purely deterministic superfluid simulation of a dotwave in a harmonic potential ( dot attached to a spring, no viscous dissipation, D=0), the dot has successive clockwise and anti-clockwise circle-like motions, separated by intermittences with null mean angular momentum
Surfer DotWave attached to a spring moving with no viscosity
Surfer attached to a spring moving with no viscosity
Integration of motion equation is done continuously via matlab DELAY DIFERENTIAL EQUATION (ddesd) solver
Hence, the dot “reads” continuously the value of the field
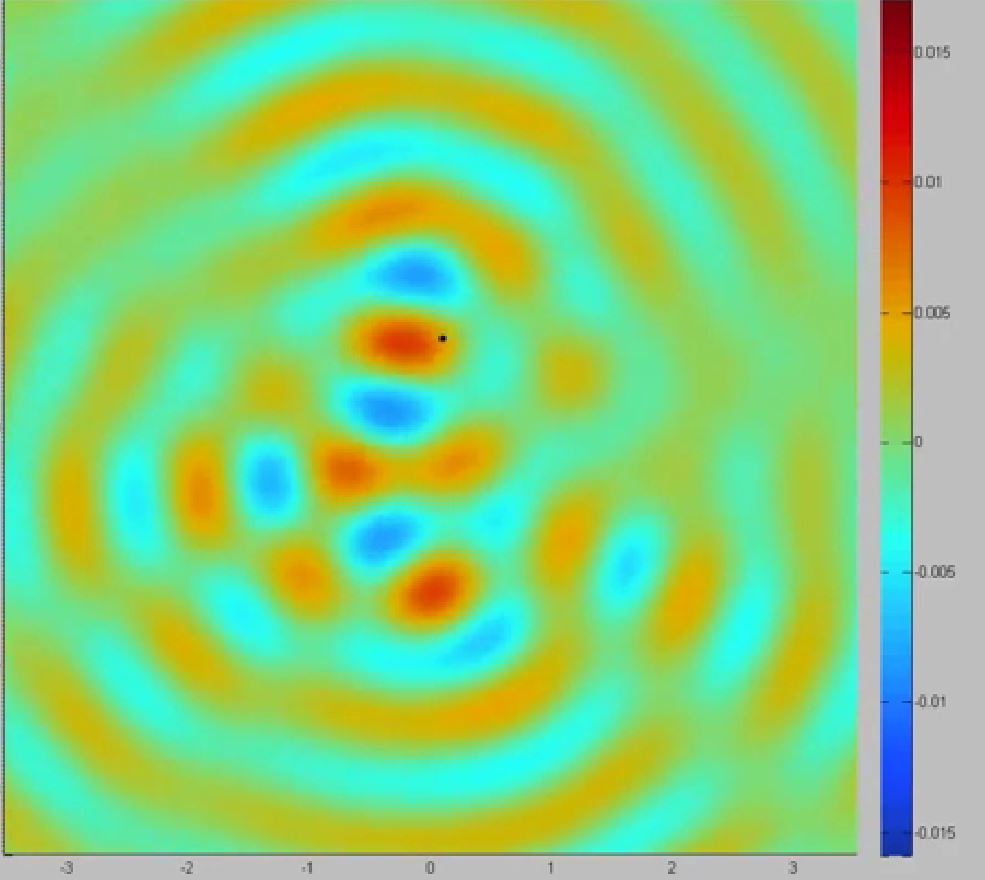
In the mean time, the dot “writes” to the field evry T_F (that is a “bounce”) : at each bounce, a local wave field represented by a Bessel JO function is created, which is then slowly damped (That is the memory Me parameter)
Interferences between the waves created by the last previous 300 bounces (THAT IS THE CUTOFF parameter) are computed at each integration step to obtain the shape of the wave and the motion of the dot.
Particle in a box – DotWave Self-Interference tracking and statistics
Wave particle in a 1-D box, tracking and statistics
particle-Wave in a ring : a Dotwave Collisionner
Could such a setup be used to create a microfluidic “in-a-droplet” chemical reactor mixer ?
Classical analog of quantum eigenstate – Orbits and trajectory level
On this video, you’ll see :
– How 2 dotwaves can synchronize on 2 orbits
– How a dotwave can change his orbit (with a little help from the experimentator)
Video shot with a 30 Hz camera, at a forcing frequency of 60 Hz, hence not much stroboscopic flickering
The bath is excited just at the Faraday llevel, or slighly upper.
Dotwave in a box : emergence of normal mode
On this video, the walking droplet is confined in a small cavity (Approx. 6 to 8 times the faraday wavelength)
We observe the emergence of several normal modes of vibration of a walking droplet in a circular corral.
At first, the movement seems “random”, then, the whole wave-particle system synchronizes, and starts turning alltogether.
Differrent modes are possible, with different radius for the droplet trajectory : on this video we see a mode with the droplet on a large radius trajectory, and also a mode where the droplet is on a short radius trajectory
Its seems that thoses radius coincide with with the knots ofs thefaraday standing waves of the cavity, hence we have a quantization of the radius of the different trajectories.
2 walking droplets getting attracted
When two walking droplets start turning around each other, the distance between them is n times the wavelength (with n an integer) plus a constant.
“Tunnel effect “
Walking droplet trapped in a square box escapes after many rebounds.
( Watch a “tunnel effect” at 2’30)
Walking droplet X800 progressive slow motion
Trapped in a circular box, shot at 1000 frames per second .
Interference at double slit
A single particle creates waves that interfere after passing through two slits.