Dubertrand, R., Hubert, M., Schlagheck, P., Vandewalle, N., Bastin, T., & Martin, J. (2016). Scattering theory of walking droplets in the presence of obstacles. arXiv preprint arXiv:1605.02370.
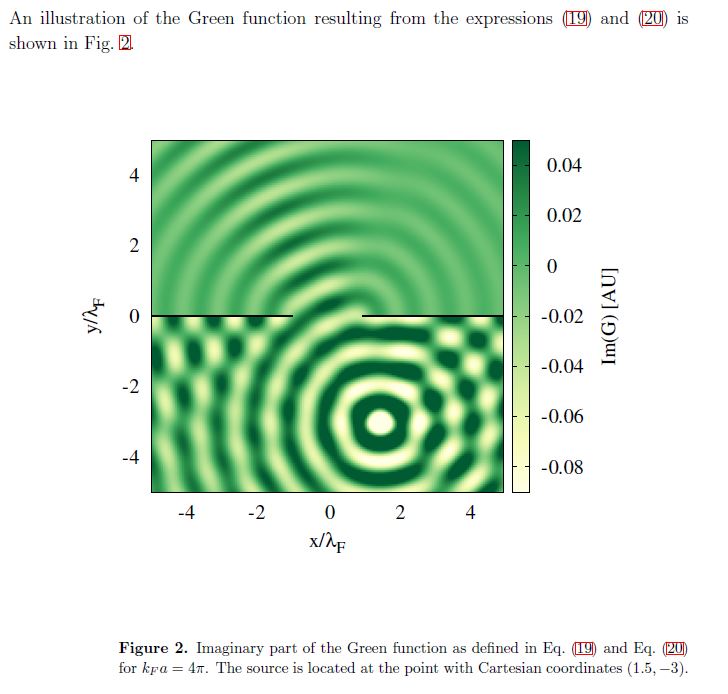
We aim to describe a droplet bouncing on a vibrating bath. Due to Faraday instability a surface wave is created at each bounce and serves as a pilot wave of the droplet. This leads to so called walking droplets or walkers. Since the seminal experiment by Couder et al [Phys. Rev. Lett. 97, 154101 (2006)] there have been many attempts to accurately reproduce the experimental results. Here we present a simple and highly versatile model inspired from quantum mechanics. We propose to describe the trajectories of a walker using a Green function approach. The Green function is related to Helmholtz equation with Neumann boundary conditions on the
obstacle(s) and outgoing conditions at infinity. For a single slit geometry our model is exactly solvable and reproduces some general features observed experimentally. It
stands for a promising.