Shedding light on pilot-wave phenomena
Brun, P. T., Harris, D. M., Prost, V., Quintela, J., & Bush, J. W. (2016). Shedding light on pilot-wave phenomena. Physical Review Fluids, 1(5), 050510.
ABSTRACT
This paper is associated with a video winner of a 2015 APS/DFD Gallery of Fluid Motion Award. The original video is available from the Gallery of Fluid Motion,
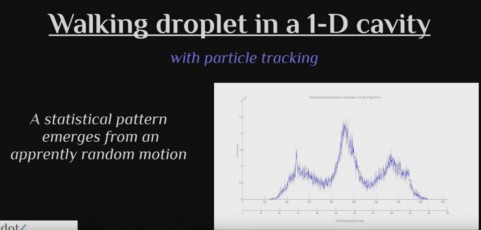
emergence of statistical pattern in a 1D cavity
On this video you will see how a walking droplet in a small 1D cavity moves “randomly” if the memory of the system is high enough (ie if the forcing is strong enough, but still below the Faraday Thresold)
And how a statistical pattern emerges with time
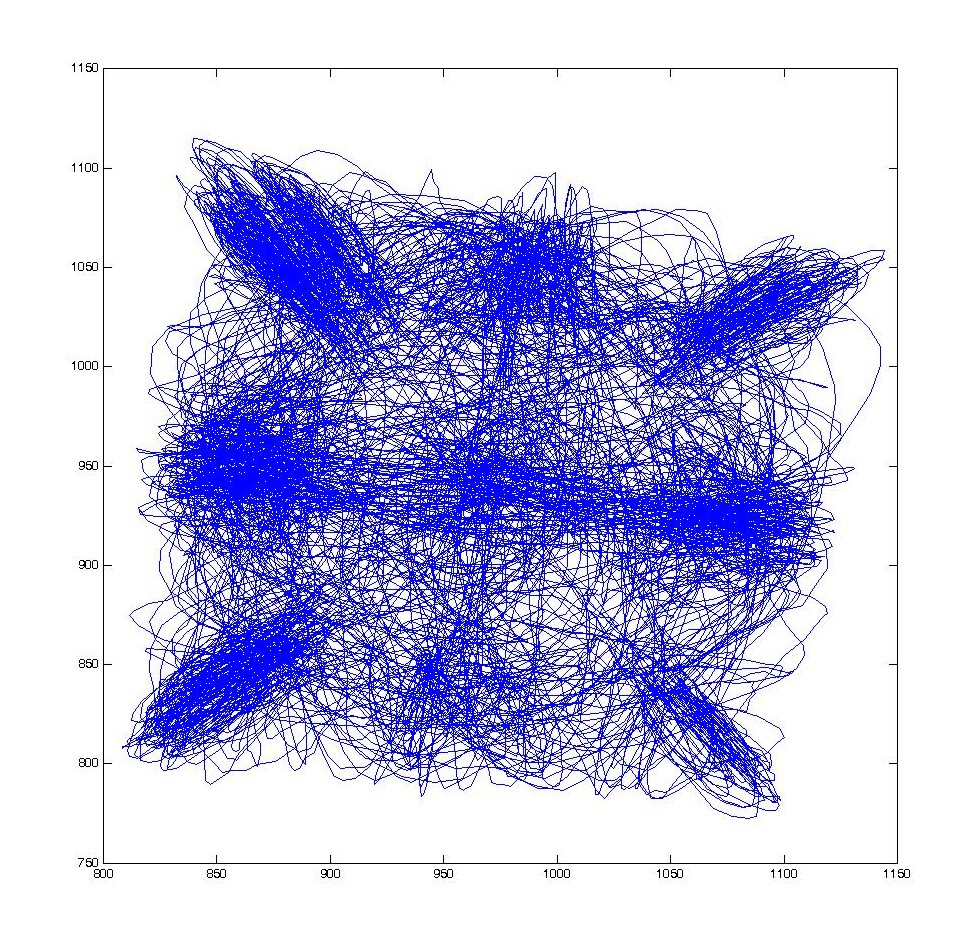
Square cavity
Read MoreEmergent quantization in a square box
Goal of the experiment :
A walking droplet is placed in a square box, at the onset of Faraday thresold.
The trajectory of the droplet is mapped.
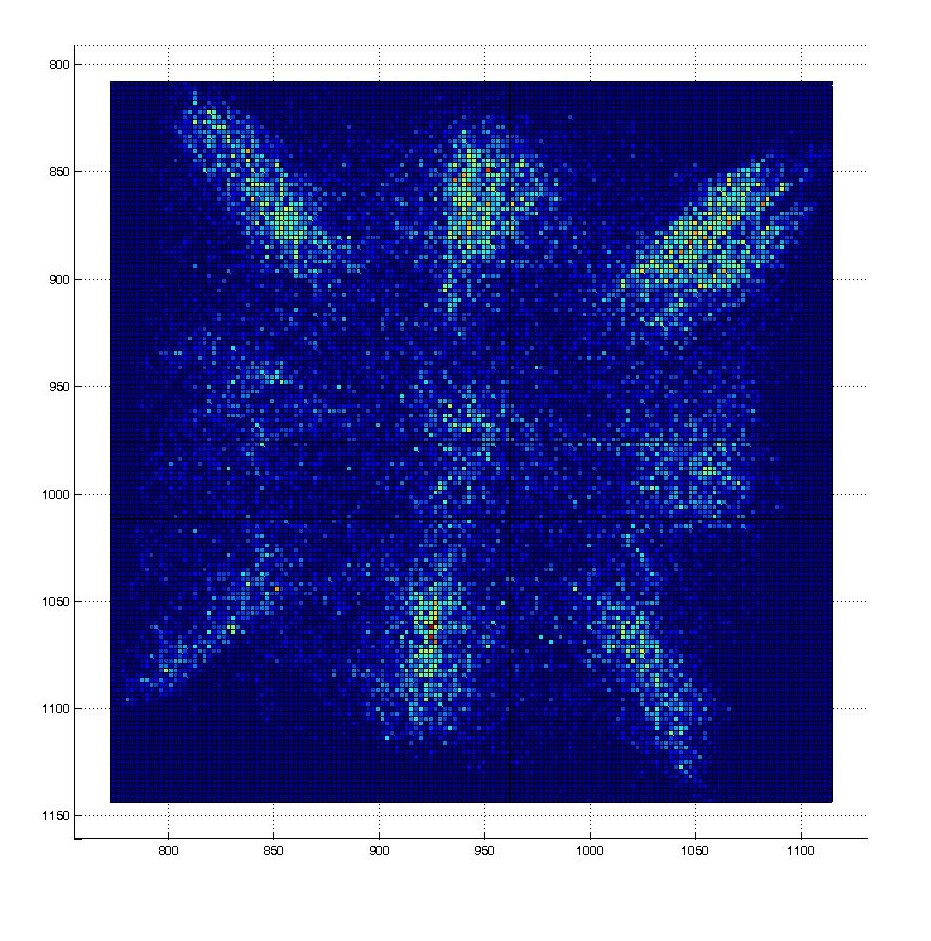
In the long time limit, does a self-interference pattern appear ? what’s its shape ? How does it relate to the square cavity surface wave eigen-modes ?
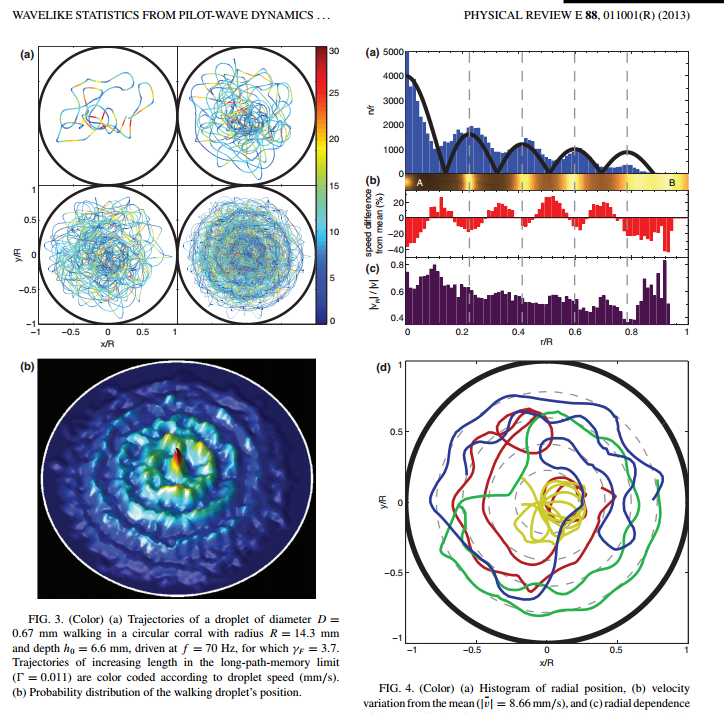
cf. experiment by Bush et al. : in a circular corral
http://dotwave.org/wavelike-statistics-from-pilot-wave-dynamics-in-a-circular-corral/
In short, we try to reproduce the experiment of Bush et al, but in a square box.
First result :
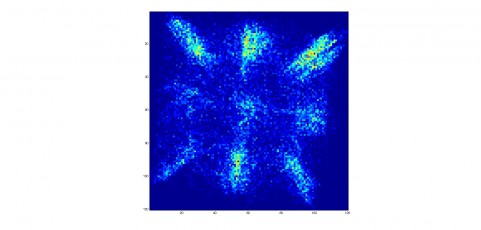
A walking droplet in a square cavity shows random motion, but with time, its trajectory is building a statistic reminiscent of the resonant mode of the cavity.
This can be seen by the naked eye in this movie excerpt :
This is then confirmed with optical tracking measurment of the trajectory :
The position distribution (~probability density) is then computed :
PDF Version of this résumé :
Emergent quantization of trajectories in a square box
Birth of a dotwave (Un rebond peut en cacher un autre)
Read MoreVideo Lesson – 07/06/2013 – Hydrodynamic Modelling of Pilot-Wave and boucing droplet coupling in a Faraday Problem
“Recent experiments by two groups, Yves Couder (Paris) and John
Bush (MIT) have shown experimentally that droplets will bounce on the
surface of a vertically vibrated bath (instead of coalescing with it),
generating a Faraday-type wavefield at every bounce. From this state, a
pitchfork symmetry breaking bifurcation leads to a “walking” state whereby
the bouncing droplet is “guided” by the self-generated wavefield – the
droplet’s pilot wave. Once this state is achieved a large array of
interesting dynamics ensues with surprising analogies to quantum
mechanical behaviour. We will present a coupled particle-fluid model that
can can be used simulate the dynamics of this problem. This is joint work
with John Bush, Andre Nachbin (IMPA) and Carlos Galeano (IMPA)”
Bouncing droplet project — single-slit diffraction
A video from TAFLAB at Berkeley University
SPH Simulation of a walking droplet
A new kind of simulation using Smoothed particle hydrodynamics by Diego Molteni, Università degli studi di Palermo, Dipartimento di Fisica e Chimic
https://www.youtube.com/watch?v=CTB4MyB07gc
Influence of a local change of depth on the behavior of bouncing oil drops
Carmigniani, R., Lapointe, S., Symon, S., & McKeon, B. J. (2013). Influence of a local change of depth on the behavior of bouncing oil drops. arXiv preprint arXiv:1310.2662.
http://arxiv.org/pdf/1310.2662.pdf
Full (Subscription required) : http://www.sciencedirect.com/science/article/pii/S0894177713003038
From caltech Mc Keon Research Group : http://www.mckeon.caltech.edu/publications/journal.html
Abstract :
The work of Couder et al [1] (see also Bush et al [3, 4]) inspired consideration of the impact of a submerged obstacle, providing a local change of depth, on the behavior of oil drops in the bouncing regime. In the linked videos, we recreate some of their results for a drop bouncing on a uniform depth bath of the same liquid undergoing vertical oscillations just below the conditions for Faraday instability, and show a range of new behaviors associated with change of depth.
This article accompanies a uid dynamics video entered into the Gallery of Fluid Motion of the 66th Annual Meeting of the APS Division of Fluid Dynamics.
And a very interesting video showing the influence of depth on the trajectory :
https://www.youtube.com/watch?v=9874AOwl1pQ
Source : http://arxiv.org/src/1310.2662v1/anc/V102356_InfluenceLocalChangeDepth_BouncingDrop.mp4
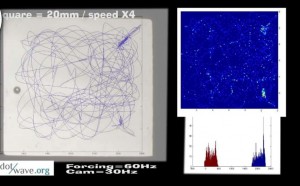
Dotwave @ 240 frame per Seconds with modified GoPro
This is how precise my temporal resolution can be with my modified goPro and (at last) a good lens : 240 fps ( @848×480 )
Forcing freq is 60 Hz, so Faraday Freq is 30Hz, so for the usual walking mode we have 8 frame during the period of the vertical dynamic. Hence we can observe the dynamic without any strobe effect.
Question: What is the (m, n) mode of the first droplet shown in the movie ?
Dotwave Sonification
Even if the ear cannot detect any transition on this one, it might give somebody … ideas ?
( Sound is the derivative of the sum of all field values at the center )
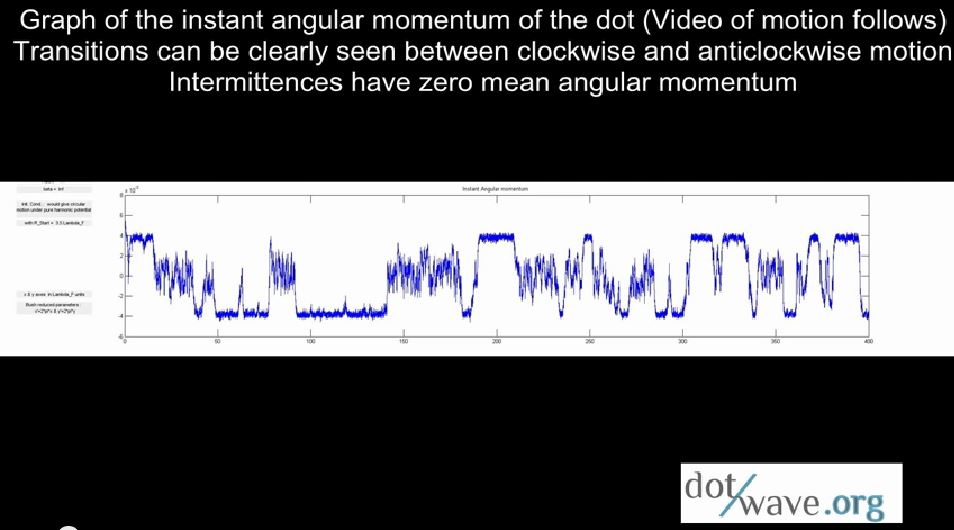
Spin Inversion : deterministic & chaotic superposition
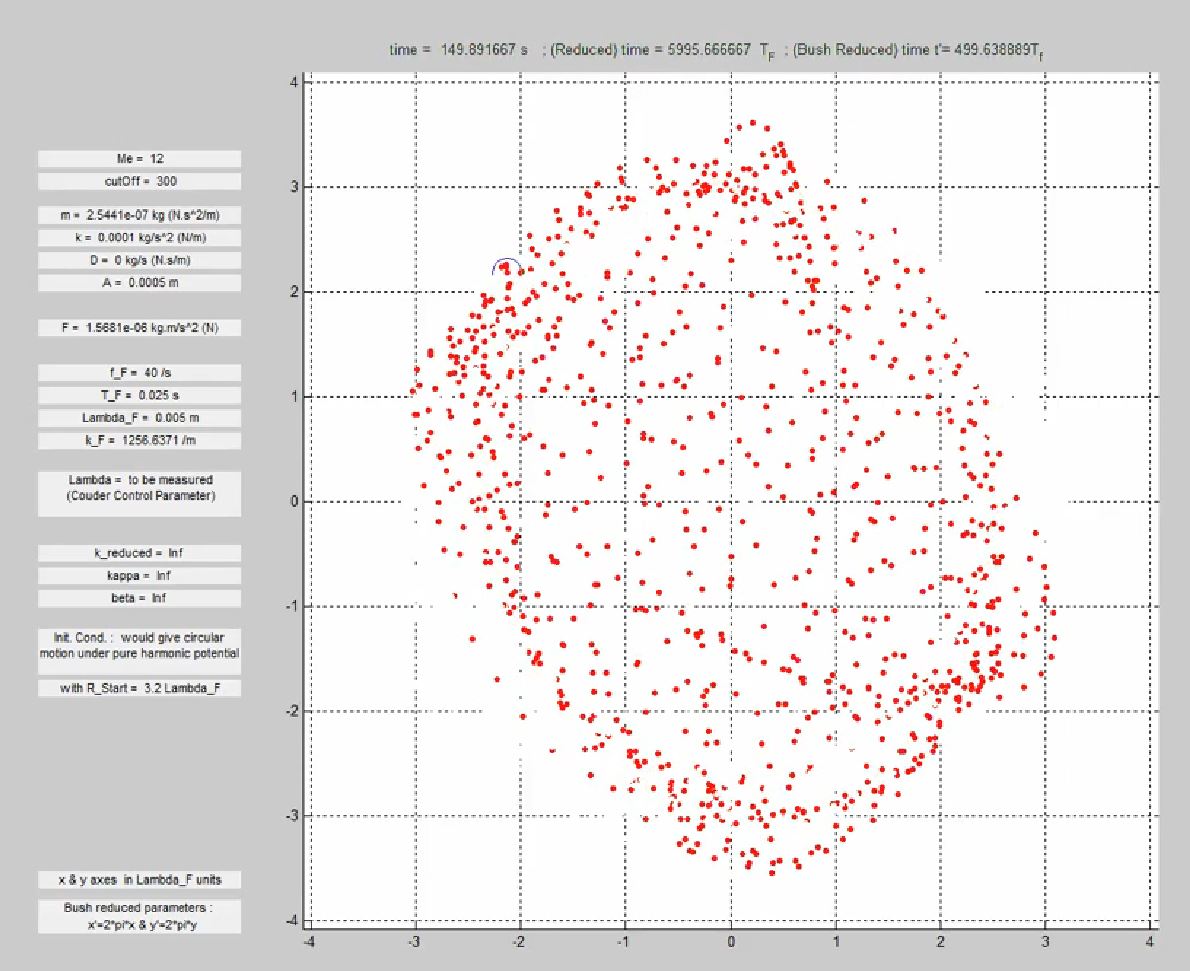
Surfer DotWave attached to a spring moving with no viscosity
Surfer attached to a spring moving with no viscosity
Integration of motion equation is done continuously via matlab DELAY DIFERENTIAL EQUATION (ddesd) solver
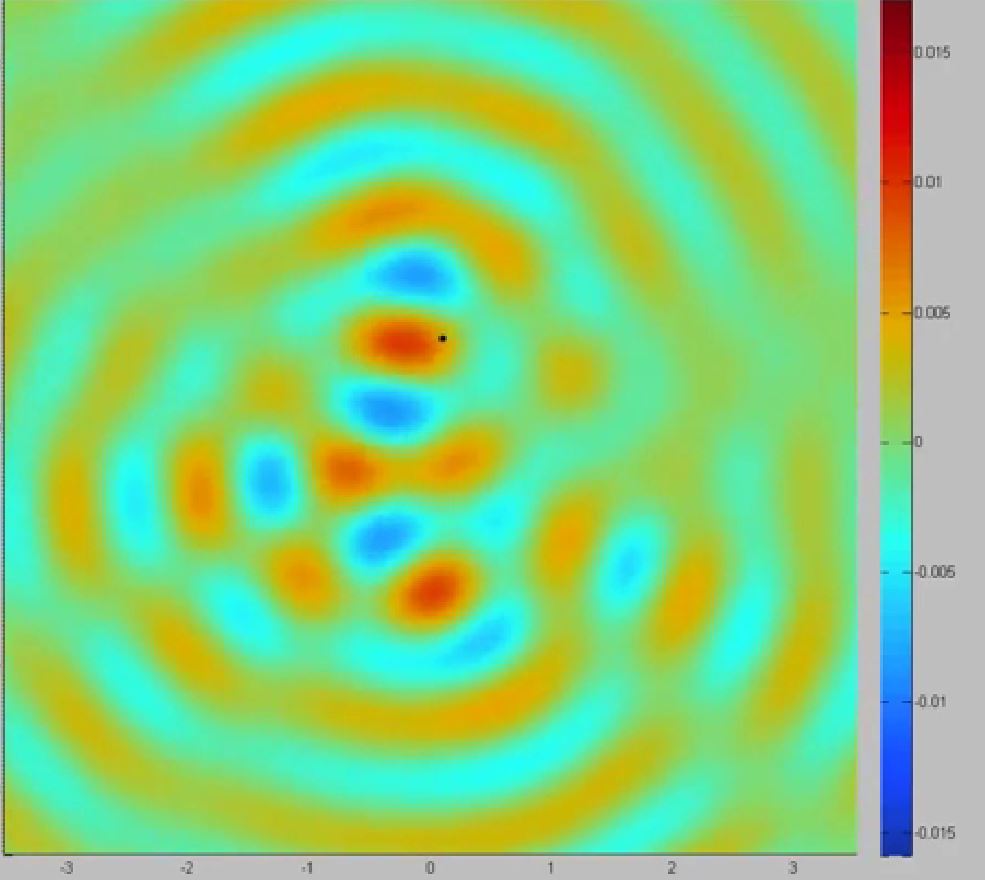
Hence, the dot “reads” continuously the value of the field
In the mean time, the dot “writes” to the field evry T_F (that is a “bounce”) : at each bounce, a local wave field represented by a Bessel JO function is created, which is then slowly damped (That is the memory Me parameter)
Interferences between the waves created by the last previous 300 bounces (THAT IS THE CUTOFF parameter) are computed at each integration step to obtain the shape of the wave and the motion of the dot.
Spin Inversions
On this purely deterministic superfluid simulation of a dotwave in a harmonic potential ( dot attached to a spring, no viscous dissipation, D=0), the dot has successive clockwise and anti-clockwise circle-like motions, separated by intermittences with null mean angular momentum
Particle in a box – DotWave Self-Interference tracking and statistics
Read MoreDotwave in a monodimensionnal box
Read MoreDotWaves interactions
Read Moreparticle-Wave in a ring : a Dotwave Collisionner
Read MoreClassical analog of quantum eigenstate – Orbits and trajectory level
On this video, you’ll see :
– How 2 dotwaves can synchronize on 2 orbits
– How a dotwave can change his orbit (with a little help from the experimentator)
Video shot with a 30 Hz camera, at a forcing frequency of 60 Hz, hence not much stroboscopic flickering
The bath is excited just at the Faraday llevel, or slighly upper.