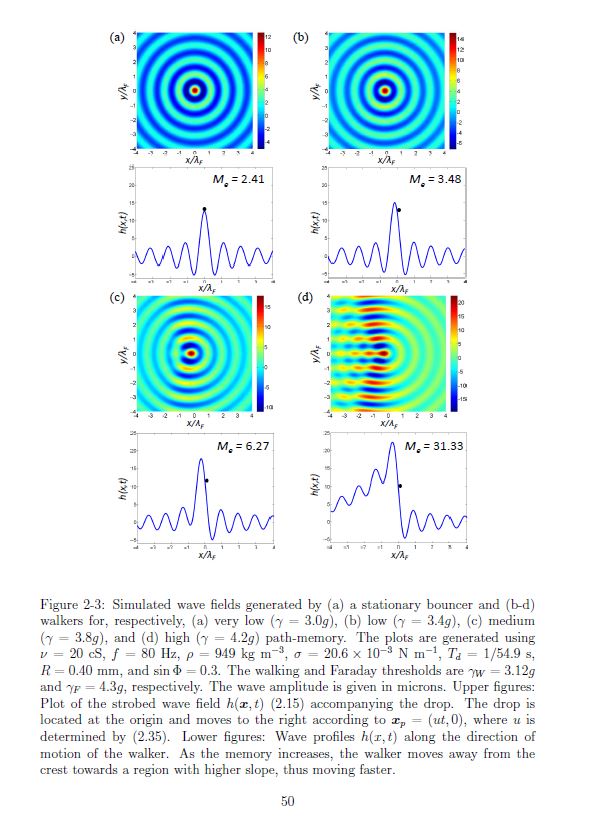
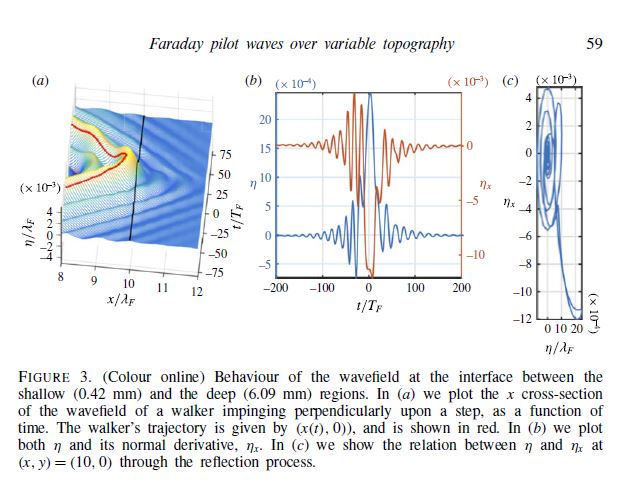
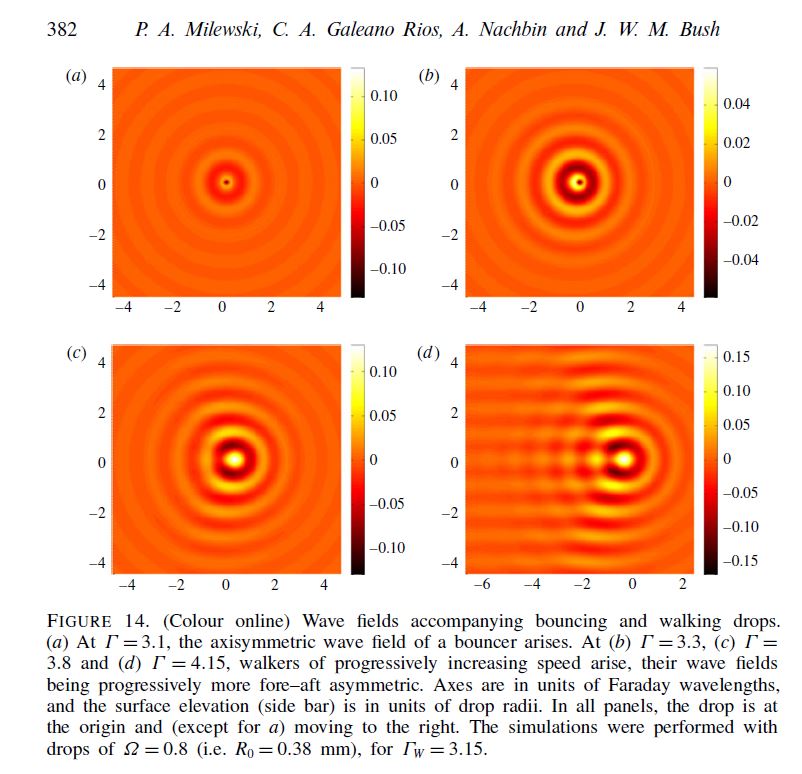
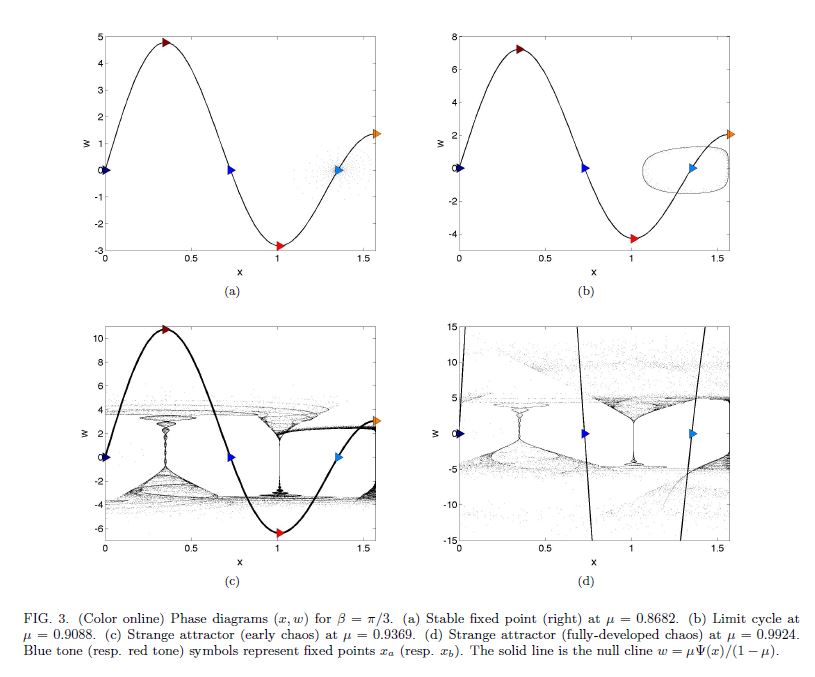
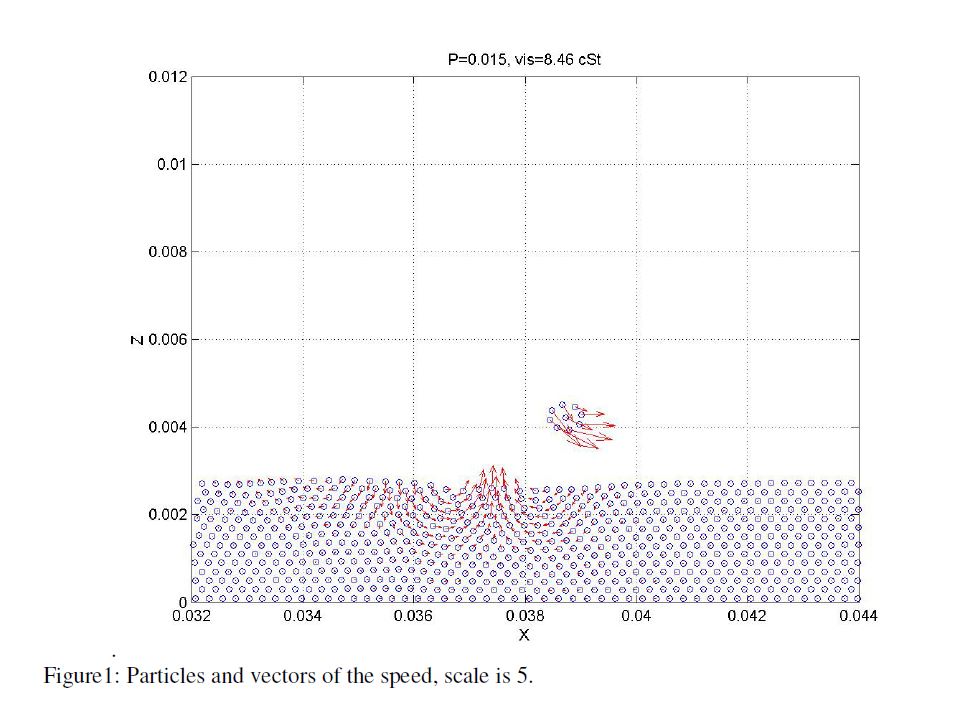
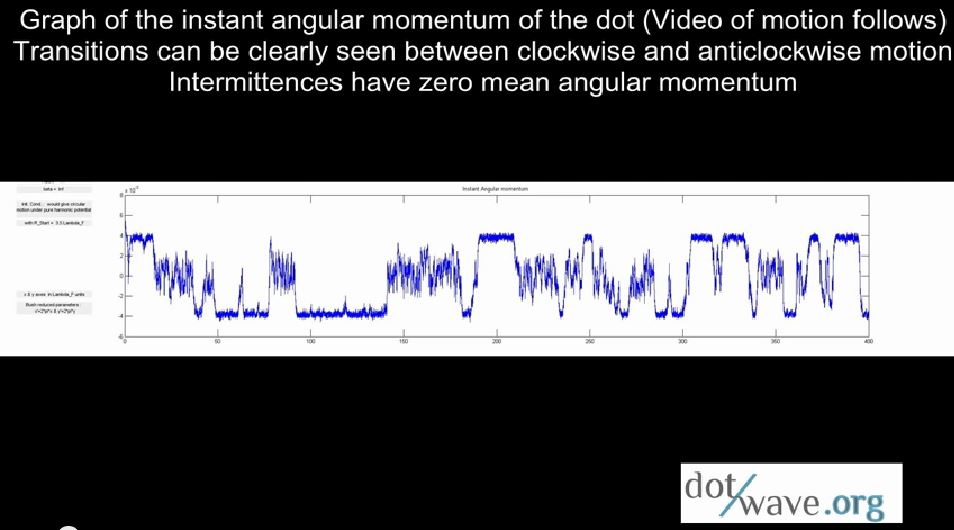
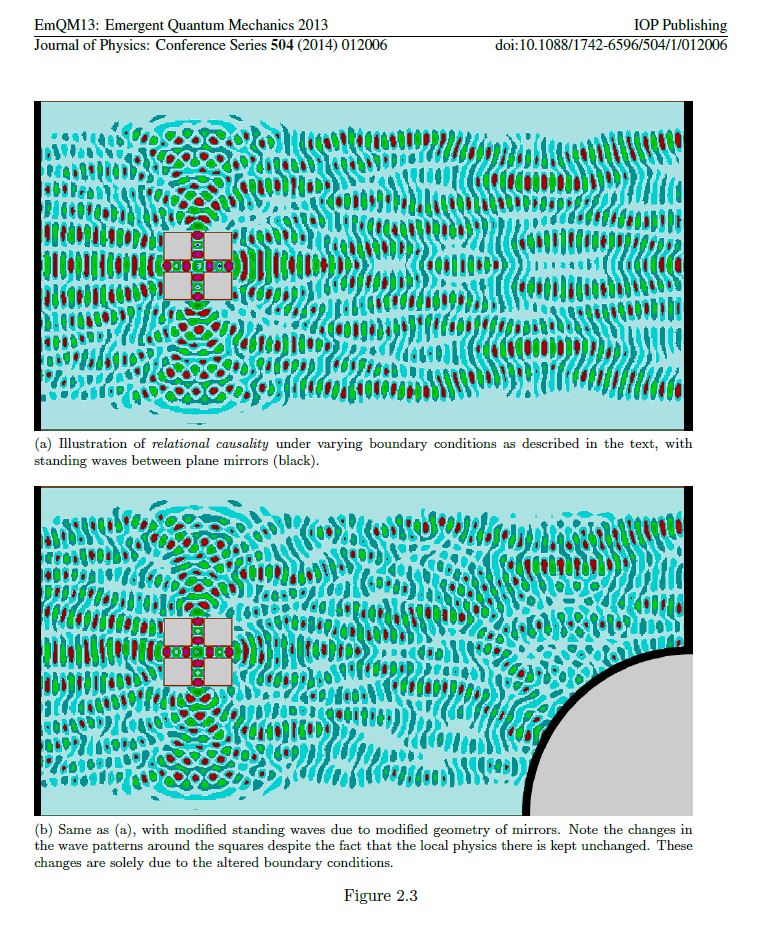
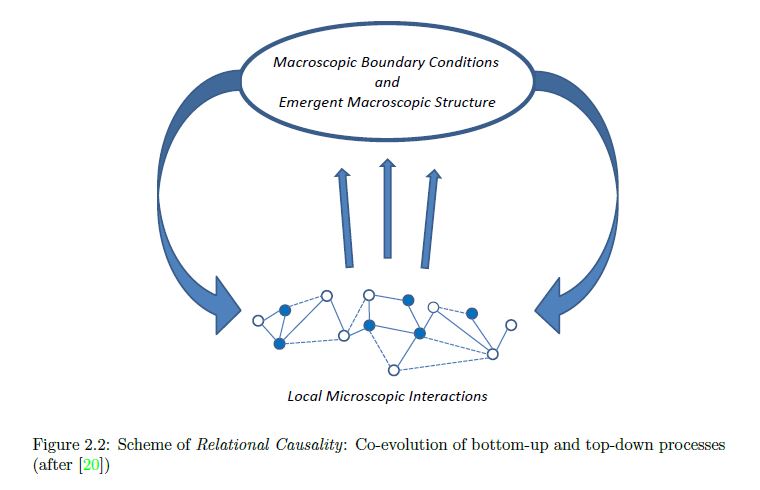
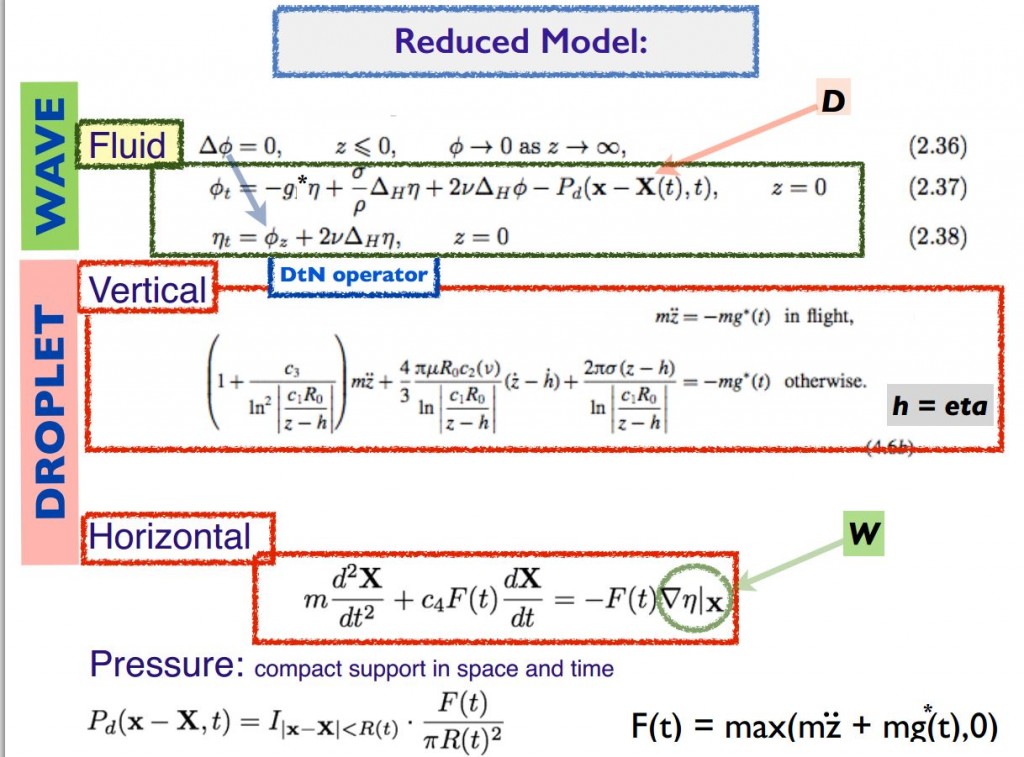
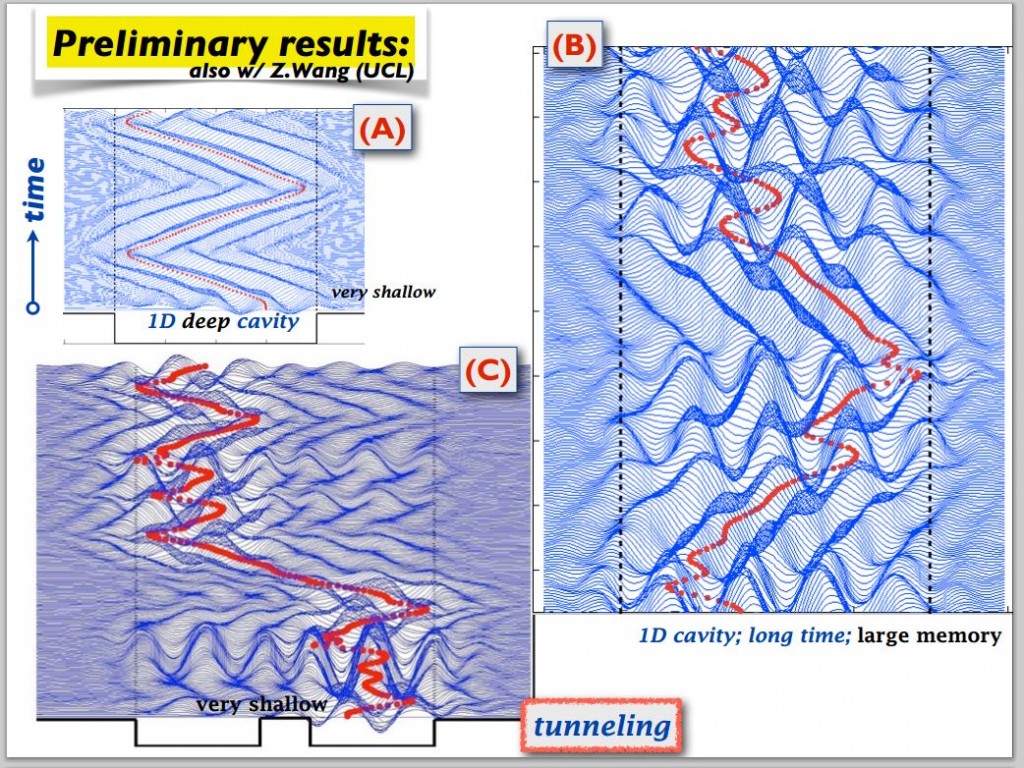
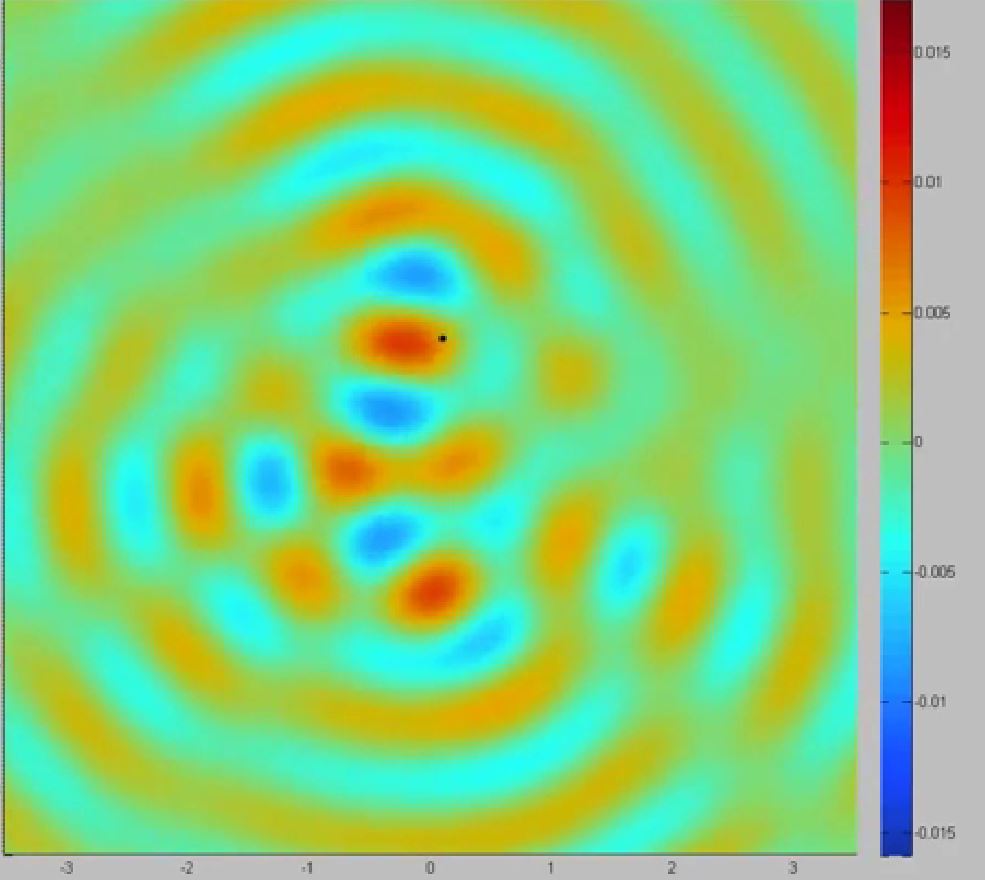
ABSTRACT  : “Yves Couder and coworkers have demonstrated that millimetric droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic quantum realm, including single-particle diffraction, tunneling, quantized orbits, and wave-like statistics in a corral. We here develop an integro-differential trajectory equation for these walking droplets with a view to gaining insight into their subtle dynamics. The orbital quantization is rationalized by assessing the stability of the orbital solutions. The stability analysis also predicts the existence of wobbling orbital states reported in recent experiments, and the absence of stable orbits in the limit of large vibrational forcing. In this limit, the complex walker dynamics give rise to a coherent statistical behavior with wave-like features. We characterize the progression from quantized orbits to chaotic dynamics as the vibrational forcing is increased progressively. We then describe the dynamics of a weakly-accelerating walker in terms of its wave-induced added mass, which provides rationale for the anomalously large orbital radii observed in experiments.”

Oza, A. U. (2014). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory (Doctoral dissertation, Massachusetts Institute of Technology).

https://dspace.mit.edu/bitstream/handle/1721.1/90191/890211673-MIT.pdf?sequence=2

Abstract : Couder et al. (Nature, vol. 437 (7056), 2005, p. 208) discovered that droplets walking on a vibrating bath possess certain features previously thought to be exclusive to quantum systems. These millimetric droplets synchronize with their Faraday wavefield, creating a macroscopic pilot-wave system. In this paper we exploit the fact that the waves generated are nearly monochromatic and propose a hydrodynamic model capable of quantitatively capturing the interaction between bouncing drops and a variable topography. We show that our reduced model is able to reproduce some important experiments involving the drop–topography interaction, such as non-specular reflection and single-slit diffraction.

Faria, L. M. (2017). A model for Faraday pilot waves over variable topography. Journal of Fluid Mechanics, 811, 51-66.

https://www.cambridge.org/

Abstract  : We examine the orbital dynamics of droplets self-propelling along the surface of a vibrating bath. Circular orbital motion may arise when the walking droplet is subjected to one of three external force fields, the Coriolis force, a simple harmonic force, and a Coulomb force. Particular attention is given to a theoretical characterization of the onset of chaos that accompanies the destabilization of such circular orbits.

Tambasco, L., Harris, D., Oza, A., Rosales, R., & Bush, J. (2015, November). Onset of chaos in orbital pilot-wave dynamics. In APS Meeting Abstracts.

Paper available on researchgate.net/ (Requires free login)

Milewski, P. A., Galeano-Rios, C. A., Nachbin, A., & Bush, J. W. (2015). Faraday pilot-wave dynamics: modelling and computation. Journal of Fluid Mechanics, 778, 361-388.

A millimetric droplet bouncing on the surface of a vibrating fluid bath can self-propel by virtue of a resonant interaction with its own wave field. This system represents the first known example of  pilot-wave system of the form envisaged by Louis de Broglie in his double-solution pilot-wave theory. We here develop a fluid model of pilot-wave hydrodynamics by coupling recent models of the droplet’s bouncing dynamics with a more realistic model of weakly viscous quasi-potential wave generation and evolution. The resulting model is the first to capture a number of features reported in experiment, including the rapid transient wave generated during impact, the Doppler effect and walker–walker interactions.

https://www.researchgate.net/profile/Paul_Milewski/publication/281111731_Faraday_pilot-wave_dynamics_Modelling_and_computation/links/55ebf4b208ae21d099c5ec8a.pdf

Gilet, T. (2014). Dynamics and statistics of wave-particle interactions in a confined geometry. Physical Review E, 90(5), 052917.

A walker is a droplet bouncing on a liquid surface and propelled by the waves that it generates. This macroscopic wave-particle association exhibits behaviors reminiscent of quantum particles. This article presents a toy model of the coupling between a particle and a confined standing wave. The resulting 2D iterated map captures many features of the walker dynamics observed in different configurations of confinement. These features include the time decomposition of the chaotic trajectory in quantized eigenstates, and the particle statistics being shaped by the wave. It shows that deterministic wave-particle coupling expressed in its simplest form can account for some quantumlike behaviors.

https://orbi.ulg.ac.be/bitstream/2268/178755/2/Generic.pdf

Molteni, D., Vitanza, E., & Battaglia, O. R. (2016). Smoothed Particles Hydrodynamics numerical simulations of droplets walking on viscous vibrating fluid. arXiv preprint arXiv:1601.05017.

Abstract :

“We study the phenomenon of the “walking droplet”, by means of numerical fluid dynamics simulations using a standard version of the Smoothed Particle Hydrodynamics method. The phenomenon occurs when a millimetric drop is released on the surface of an oil of the same composition contained in a container subjected to vertical oscillations of frequency and amplitude close to the Faraday instability threshold. At appropriate values of the parameters of the system under study, the liquid drop jumps permanently on the surface of the vibrating fluid forming a localized wave-particle system, reminding the behavior of a wave particle quantum system as suggested by de Broglie. In the simulations, the drop and the wave travel at nearly constant speed, as observed in experiments. In our study we made relevant simplifying assumptions, however we observe that the wave-drop coupling is easily obtained. This fact suggests that the phenomenon may occur in many contexts and opens the possibility to study the phenomenon in an extremely wide range of physical configurations.”

http://arxiv.org/ftp/arxiv/papers/1601/1601.05017.pdf

A new kind of simulation using Smoothed particle hydrodynamics by Diego Molteni, Università degli studi di Palermo, Dipartimento di Fisica e Chimic

Even if the ear cannot detect any transition on this one, it might give somebody … ideas ?

( Sound is the derivative of the sum of all field values at the center )

On this purely deterministic superfluid simulation of a dotwave in a harmonic potential ( dot attached to a spring, no viscous dissipation, D=0), the dot has successive clockwise and anti-clockwise circle-like motions, separated by intermittences with null mean angular momentum

Grössing, G., Fussy, S., Pascasio, J. M., & Schwabl, H. (2014, April). Relational causality and classical probability: Grounding quantum phenomenology in a superclassical theory. In Journal of Physics: Conference Series (Vol. 504, No. 1, p. 012006). IOP Publishing.

Abstract. : By introducing the concepts of \superclassicality” and \relational causality”, it is shown here that the velocity eld emerging from an n-slit system can be calculated as an
average classical velocity eld with suitable weightings per channel. No deviation from classical probability theory is necessary in order to arrive at the resulting probability distributions.
In addition, we can directly show that when translating the thus obtained expression for said velocity eld into a more familiar quantum language, one immediately derives the basic
postulate of the de Broglie-Bohm theory, i.e. the guidance equation, and, as a corollary, the exact expression for the quantum mechanical probability density current. Some other direct
consequences of this result will be discussed, such as an explanation of Born’s rule and Sorkin’s first and higher order sum rules, respectively.

http://iopscience.iop.org/1742-6596/504/1/012006/pdf/1742-6596_504_1_012006.pdf

classical probability theory

n-slit system

guidance equation

Analysis of currrent state of the art modelling

Reflexions in a 1D Cavity

Computer simulations

(proceedings of RIO 2014  workshop)

http://www.personal.psu.edu/alm24/IMPA/talks/IMPANachbin.pdf

Shirokoff, D. (2013). Bouncing droplets on a billiard table. Chaos: An Interdisciplinary Journal of Nonlinear Science, 23(1), 013115.

http://arxiv.org/pdf/1203.2204.pdf

Discrete numerical simulation

Attractor ets

In this PDF, you will find the equation of motion used in the numerical simulation, based on the work of BUSH et al. from the MIT team.

DotWaveSimulation

Surfer attached to a spring moving with no viscosity

Integration of motion equation is done continuously via matlab DELAY DIFERENTIAL EQUATION (ddesd) solver

Hence, the dot “reads” continuously the value of the field

In the mean time, the dot “writes” to the field evry T_F (that is a “bounce”) : at each bounce, a local wave field represented by a Bessel JO function is created, which is then slowly damped (That is the memory Me parameter)

Interferences between the waves created by the last previous 300 bounces (THAT IS THE CUTOFF parameter) are computed at each integration step to obtain the shape of the wave and the motion of the dot.

On this purely deterministic superfluid simulation of a dotwave in a harmonic potential ( dot attached to a spring, no viscous dissipation, D=0), the dot has successive clockwise and anti-clockwise circle-like motions, separated by intermittences with null mean angular momentum

Oza, A. U., Rosales, R. R., & Bush, J. W. (2013). A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. Journal of Fluid Mechanics,737, 552-570.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/12/ORB-JFM.pdf

Integro-differential equation describing the horizontal motion of a walking droplet

Stability to perturbations

Moláček, J., & Bush, J. W. (2013). Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory. Journal of Fluid Mechanics, 727, 582-617.

http://math.mit.edu/~bush/wordpress/wp-content/uploads/2013/07/MB2-2013.pdf

The most advanced theoretical model