Gilet, T. (2014). Dynamics and statistics of wave-particle interactions in a confined geometry. Physical Review E, 90(5), 052917.
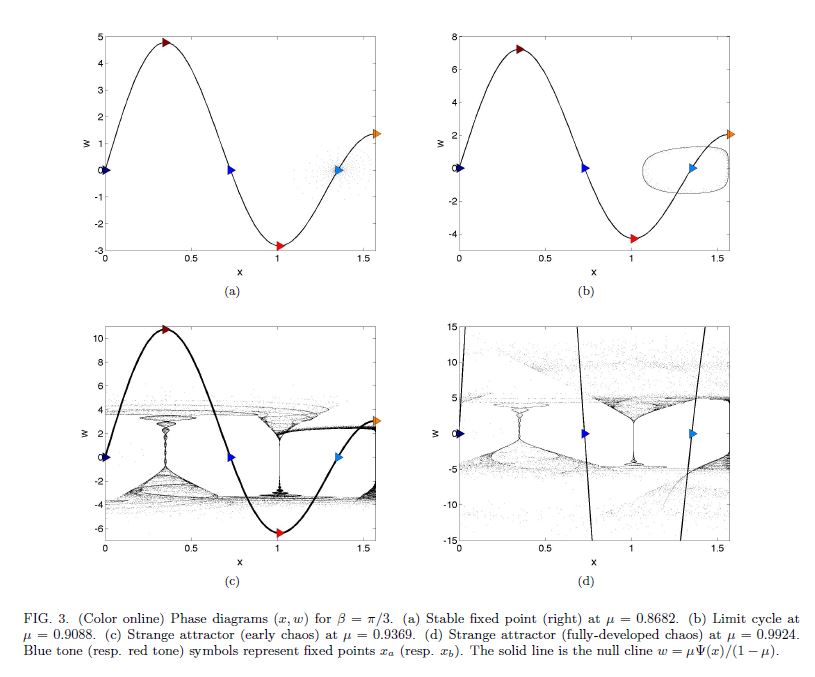
A walker is a droplet bouncing on a liquid surface and propelled by the waves that it generates. This macroscopic wave-particle association exhibits behaviors reminiscent of quantum particles. This article presents a toy model of the coupling between a particle and a confined standing wave. The resulting 2D iterated map captures many features of the walker dynamics observed in different configurations of confinement. These features include the time decomposition of the chaotic trajectory in quantized eigenstates, and the particle statistics being shaped by the wave. It shows that deterministic wave-particle coupling expressed in its simplest form can account for some quantumlike behaviors.
https://orbi.ulg.ac.be/bitstream/2268/178755/2/Generic.pdf